LSER Models for Solubility Determination: A Comprehensive Guide for Pharmaceutical Scientists

Abstract

This article provides a comprehensive exploration of Linear Solvation Energy Relationship (LSER) models for determining solubility parameters, a critical task for researchers and drug development professionals. It covers the foundational theory behind LSERs, including their molecular descriptors and thermodynamic basis. The content details practical methodologies for model application in pharmaceutical contexts, such as predicting drug solubility with macrocyclic hosts and excipient compatibility. It addresses common challenges and optimization strategies, including the integration of computational tools like COSMO-RS and data-driven machine learning. Finally, the article offers validation frameworks and comparative analyses with traditional approaches like Hansen Solubility Parameters, empowering scientists to reliably apply LSERs in drug formulation and material science.

Understanding LSER Fundamentals: From Solubility Parameters to Molecular Descriptors

The accurate prediction of solubility behavior is a cornerstone of research and development in fields ranging from polymer science to pharmaceutical development. The journey from the Hildebrand Solubility Parameter to the Hansen Solubility Parameters (HSP) represents a critical evolution in the application of Linear Solvation Energy Relationship (LSER) principles for quantifying molecular interactions. This progression from a one-dimensional to a three-dimensional model has transformed solubility from a qualitative concept of "like dissolves like" into a quantitative, predictive framework that accounts for the multiple facets of molecular cohesion. Within LSER research, solubility parameters serve as practical thermodynamic tools that bridge molecular structure with macroscopic solution behavior, enabling researchers to make informed predictions about phase equilibria, polymer dissolution, and formulation stability without exhaustive experimental trial and error.

Historical Development and Theoretical Foundations

The Hildebrand Solubility Parameter

In 1936, Joel H. Hildebrand introduced a groundbreaking concept for predicting the solubility of non-electrolytes, including polymer materials [1] [2]. He defined the solubility parameter (δ) as the square root of the cohesive energy density (CED), which represents the energy required to remove a molecule from its neighbors per unit volume.

The parameter is mathematically defined as: δ = (ΔE_m / V_m)^(1/2) = ((ΔH_m - RT) / (M / ρ))^(1/2) where ΔEm is the molar energy of vaporization, Vm is the molar volume, ΔH_m is the molar enthalpy of vaporization, R is the gas constant, T is the absolute temperature, M is the molar mass, and ρ is the density [1].

This one-dimensional parameter was revolutionary for its time, providing the first quantitative basis for the "like dissolves like" principle. It found particular utility for non-polar and slightly polar systems without hydrogen bonding [1]. The limitations of the Hildebrand parameter became apparent when applied to polar molecules and hydrogen-bonding systems, where it often failed to accurately predict solubility behavior [3] [4].

Table 1: Hildebrand Solubility Parameters (δ) of Selected Materials

Substance	δ (cal¹⸍² cm⁻³⸍²)	δ (MPa¹⸍²)
n-Pentane	7.0	14.4
n-Hexane	7.24	14.9
Diethyl Ether	7.62	15.4
Acetone	9.77	19.9
Ethanol	12.92	26.5
Polyethylene	7.9	-
Polystyrene	9.13	-
Nylon 6,6	13.7	28

Hansen Solubility Parameters

Recognizing the limitations of the single-parameter approach, Charles M. Hansen introduced a three-dimensional solubility parameter system in his 1967 PhD thesis [5] [4]. Hansen proposed that the total cohesive energy density arises from three distinct intermolecular forces, leading to the now-familiar tripartite parameter system:

δ_t² = δ_d² + δ_p² + δ_h²

The three parameters are:

• δ_d (Dispersion parameter): Quantifies London dispersion forces arising from transient electron cloud fluctuations [5]
• δ_p (Polar parameter): Represents permanent dipole-dipole interactions (Keesom forces) [5]
• δ_h (Hydrogen bonding parameter): Captures hydrogen bond donor/acceptor capabilities [5]

This refinement allowed for a more nuanced application of LSER principles by separately accounting for different interaction mechanisms that contribute to overall solubility behavior.

The Hildebrand to Hansen Transition: A Conceptual Diagram

Quantitative Framework of Hansen Solubility Parameters

The Hansen Distance and Relative Energy Difference

The core predictive power of HSP lies in the concept of the Hansen distance (Rₐ), which quantifies the similarity between two materials in the three-dimensional Hansen space [5] [6]. The distance is calculated as:

Rₐ² = 4(δ_d2 - δ_d1)² + (δ_p2 - δ_p1)² + (δ_h2 - δ_h1)²

The factor of 4 applied to the dispersion term difference is an empirical correction that Hansen found necessary to balance the relative contributions of the different forces, reflecting that dispersion energy contributions are approximately twice as significant as polar or hydrogen bonding contributions in determining solubility [5].

The Relative Energy Difference (RED) provides a normalized measure of solubility potential:

RED = Rₐ / R₀

Where Râ‚€ is the interaction radius of the solute material, determined experimentally [6]. The interpretation is straightforward:

• RED < 1.0: Solvent likely dissolves solute (good solvent)
• RED ≈ 1.0: Borderline solubility/swelling may occur
• RED > 1.0: Solvent unlikely to dissolve solute (poor solvent) [6]

Table 2: Hansen Solubility Parameters (in MPa¹⸍²) of Common Substances

Substance	δ_d	δ_p	δ_h	Application Notes
Water	15.5	16.0	42.3	Reference polar solvent
Ethanol	15.8	8.8	19.4	Pharmaceutical formulations
Acetone	15.5	10.4	7.0	Common laboratory solvent
Diethyl Ether	14.5	2.9	4.6	Low polarity applications
Polystyrene	18.6	6.0	4.5	Polymer processing reference
PMMA	17.7	9.1	7.1	Biomedical applications
Nafion Backbone	16.4	10.5	8.9	Fuel cell research [6]
Nafion Side Chain	15.2	11.7	15.9	Fuel cell research [6]
Cellulose	17.8	11.4	15.3	Biomass processing [7]

Comparative Performance: Hildebrand vs. Hansen

The superiority of the Hansen system is demonstrated by its ability to explain phenomena that confound the Hildebrand approach. A striking example involves epoxy dissolution [3]:

• n-Butanol and Nitroethane both have identical Hildebrand parameters (23 MPa¹⸍²) and neither dissolves a typical epoxy resin
• A 50:50 mixture of these "non-solvents" effectively dissolves the epoxy
• Hansen analysis reveals that while individually both solvents have high Rₐ values (>8), their mixture has a significantly lower Rₐ (3.9), falling within the solubility sphere of the epoxy

This phenomenon, where two non-solvents combine to form a good solvent, has been demonstrated for more than 60 solvent pairs across 22 different polymers [3].

Experimental Protocols for HSP Determination

Protocol: Determining HSP of an Unknown Polymer

Principle: The HSP values of an unknown polymer are determined by testing its solubility or swelling in a range of solvents with known HSP values, then defining a "solubility sphere" in Hansen space that contains the good solvents and excludes the poor solvents [5] [6].

Materials and Reagents:

• Polymer sample (purified, powdered when possible)
• 20-50 solvents spanning the Hansen space (see Table 3)
• Test tubes with airtight seals
• Analytical balance (±0.1 mg)
• Temperature-controlled incubation system
• Centrifuge (optional)

Table 3: Essential Solvents for HSP Determination

Solvent	δ_d	δ_p	δ_h	Role in HSP Determination
n-Hexane	14.9	0.0	0.0	Defines dispersion axis extreme
Diethyl Ether	14.5	2.9	4.6	Low polarity reference
Chloroform	17.8	3.1	5.7	Moderate dispersion
Acetone	15.5	10.4	7.0	Defines polar region
Ethanol	15.8	8.8	19.4	Hydrogen-bonding reference
Methanol	15.1	12.3	22.3	Strong hydrogen-bonding
Dimethyl Sulfoxide	18.4	16.4	10.2	High polarity solvent
Water	15.5	16.0	42.3	Defines hydrogen-bonding extreme
Ethyl Acetate	15.8	5.3	7.2	Balanced properties
N-Methyl-2-pyrrolidone	18.0	12.3	7.2	Strong polymer solvent

Procedure:

• Prepare 20-50 solutions of the polymer in selected solvents at a standard concentration (typically 1-5 mg/mL)
• Agitate mixtures continuously for 24 hours at constant temperature (typically 25°C)
• Centrifuge if necessary to separate undissolved material
• Assess solubility using:
  • Visual inspection (transparency, cloudiness)
  • Gravimetric analysis of dissolved fraction
  • Light scattering for quantitative turbidity measurement
  • Viscosity measurement for polymer solutions
• Classify solvents as "good" (complete dissolution), "partial" (swelling or partial dissolution), or "poor" (no interaction)
• Input results into HSP calculation software (e.g., HSPiP) or use graphical methods to determine the sphere center coordinates (δd, δp, δ_h) and radius (Râ‚€) that best separate good from poor solvents

Validation: Test the predicted HSP values with additional solvents not included in the initial test set. The sphere should correctly predict solubility behavior with >90% accuracy for well-behaved systems.

Protocol: Calculating HSP for Mixed Solvent Systems

Principle: The HSP of a solvent mixture can be approximated by the volume-weighted average of the component parameters [7]:

δ_mix = φ₁δ₁ + φ₂δ₂ + ... + φ_nδ_n

Where φᵢ is the volume fraction of component i.

Procedure:

• Determine the HSP values of individual solvent components from reference tables
• Calculate the volume fractions of each component in the mixture
• Compute weighted averages for each parameter:
  • δ_d(mix) = φ₁δ_d₁ + φ₂δ_d₂ + ... + φ_nδ_dn
  • δ_p(mix) = φ₁δ_p₁ + φ₂δ_p₂ + ... + φ_nδ_pn
  • δ_h(mix) = φ₁δ_h₁ + φ₂δ_h₂ + ... + φ_nδ_hn
• Use the calculated mixed HSP to determine Rₐ and RED values for target solutes

Application Example: This method enables rational design of solvent blends with desired environmental, health, and safety profiles while maintaining dissolution efficacy [5].

Research Toolkit for Solubility Parameter Studies

Essential Research Reagents and Instruments

Table 4: Research Toolkit for Solubility Parameter Determination

Tool/Reagent	Function	Application Notes
HSPiP Software	Calculates HSP from experimental data; predicts solubility	Industry standard with extensive solvent database [8]
Inverse Gas Chromatography (IGC)	Determines HSP of solids by measuring retention times of probe molecules	Provides high-accuracy data for polymers [6]
Group Contribution Methods	Estimates HSP from molecular structure	Useful preliminary screening without experiments [6]
Solvent Library	20-50 solvents spanning Hansen space	Must include representatives from all HSP regions [5]
Automated Dispensing System	Precise solvent handling for high-throughput screening	Reduces experimental error in mixture preparation
Turbidimetry System	Quantitative solubility assessment	Objective measurement of dissolution endpoints
Swelling Measurement Apparatus	Quantifies polymer swelling in marginal solvents	Important for cross-linked polymers
Cdc25A (80-93) (human)	Cdc25A (80-93) (human) Peptide	This Cdc25A (80-93) (human) peptide is for research applications only. It is not for human or veterinary diagnostic or therapeutic use. Explore its role in cell cycle studies.
Sdh-IN-13	Sdh-IN-13, MF:C19H13F7N4O, MW:446.3 g/mol	Chemical Reagent

Applications in Pharmaceutical and Materials Research

Case Study: Predicting Polymer-Solvent Interactions

The application of HSP extends across multiple disciplines, with particularly significant impact in pharmaceutical development and advanced materials. A representative case involves the optimization of fuel cell catalyst inks containing Nafion ionomer [6]. Researchers calculated dual HSP values for Nafion, recognizing its amphiphilic structure with hydrophobic backbone (δd=16.4, δp=10.5, δh=8.9) and hydrophilic side chains (δd=15.2, δp=11.7, δh=15.9). This detailed understanding enabled rational solvent selection to optimize ionomer dispersion state, which directly impacts catalyst layer structure and fuel cell performance.

Case Study: Natural Product Extraction Optimization

In natural product extraction, HSP has revolutionized solvent selection for compounds like cellulose [7]. Researchers determined that effective cellulose solvents must match its HSP profile (δd=17.8, δp=11.4, δ_h=15.3), leading to the identification of novel solvent systems including ionic liquids and deep eutectic solvents (DES). This approach has significantly reduced the traditional trial-and-error in identifying efficient, environmentally benign cellulose solvents for biomass processing.

Experimental Workflow for HSP Applications

The historical evolution from Hildebrand to Hansen Solubility Parameters represents a paradigm shift in how researchers approach solubility challenges. While Hildebrand's pioneering work established the fundamental connection between cohesive energy and solubility, Hansen's three-dimensional framework provided the necessary sophistication to address real-world systems with diverse molecular interactions. In the context of LSER model development, HSP serves as a practical implementation that successfully correlates molecular structure with macroscopic solution behavior. For today's drug development professionals and materials researchers, HSP provides a powerful predictive toolbox that reduces reliance on empirical approaches and enables rational design of formulations, extractions, and processing conditions across the chemical sciences.

Core Principles of Linear Solvation Energy Relationships (LSER)

Linear Solvation Energy Relationships (LSER) represent a powerful quantitative approach for predicting and interpreting the partitioning behavior of solutes in different chemical environments. Originally developed by Abraham, the LSER model provides a mechanistic framework for understanding how molecular interactions influence solvation properties across various phases [9] [10]. This methodology has found extensive applications in environmental chemistry, pharmaceutical sciences, and chemical engineering, particularly for predicting solubility, partition coefficients, and retention in chromatographic systems [11] [10].

The core LSER model expresses a free energy-related property as a linear combination of solute descriptors that encode specific molecular interaction capabilities. For solubility parameter determination research, LSERs offer a systematic approach to deconvoluting the relative contributions of different intermolecular forces that collectively define solubility behavior [9]. This molecular-level understanding enables researchers to make predictive assessments of solute behavior without extensive experimental measurements, streamlining the drug development process.

The LSER Equation and Molecular Descriptors

Fundamental LSER Equations

The Abraham LSER model employs two primary equations for different phase transfer processes. For solute transfer between two condensed phases, the model utilizes:

log(P) = cp + epE + spS + apA + bpB + vpVx [9]

Where P represents the partition coefficient between two condensed phases (e.g., water-to-organic solvent or alkane-to-polar organic solvent). For gas-to-solvent partitioning, the equation becomes:

log(KS) = ck + ekE + skS + akA + bkB + lkL [9]

Here, KS is the gas-to-organic solvent partition coefficient. In both equations, the capital letters (E, S, A, B, V, L) represent solute-specific molecular descriptors, while the lowercase coefficients (e, s, a, b, v, l) are system-specific parameters determined by regression analysis of experimental data [9] [10].

Solute Molecular Descriptors

Table 1: LSER Solute Molecular Descriptors and Their Chemical Significance

Descriptor	Chemical Interpretation	Molecular Property Represented
Vx	McGowan's characteristic volume	Molecular size/cavity formation energy
L	Gas-hexadecane partition coefficient at 298 K	Overall dispersion interactions
E	Excess molar refraction	Polarizability from π- and n-electrons
S	Dipolarity/polarizability	Dipole-dipole and dipole-induced dipole interactions
A	Hydrogen bond acidity	Solute's hydrogen bond donating ability
B	Hydrogen bond basicity	Solute's hydrogen bond accepting ability

These solute descriptors are considered intrinsic molecular properties that remain constant across different systems [9] [10]. The E descriptor encodes information about a solute's polarizability, particularly from π- and n-electrons, while the S descriptor represents the solute's ability to engage in dipole-type interactions [10]. The hydrogen bonding descriptors A and B quantify the solute's hydrogen bond donating and accepting capacities, respectively [9]. The V_x and L descriptors both relate to molecular size but capture different aspects of dispersion interactions and cavity formation energy [9].

System Coefficients and Their Interpretation

Table 2: LSER System Coefficients and Their Physicochemical Meaning

Coefficient	Complementary Property	Chemical Interpretation
v	Solvent cohesion	Endoergic cavity formation energy in solvent
l	Solvent dispersion	Solvent's capacity for dispersion interactions
e	Solvent polarizability	Solvent's ability to interact with solute π/n-electrons
s	Solvent dipolarity	Solvent's dipole-dipole interaction capability
a	Solvent basicity	Solvent's hydrogen bond accepting ability
b	Solvent acidity	Solvent's hydrogen bond donating ability

The system coefficients (lowercase letters) are determined through multiple linear regression analysis of experimental data for a variety of solutes with known descriptors [9] [10]. These coefficients represent the complementary effect of the solvent phase on solute-solvent interactions and contain specific chemical information about the solvent system [9]. The a and b coefficients are particularly important for understanding hydrogen-bonding interactions in solubility parameter determination, as they reflect the solvent's hydrogen bond accepting and donating capacities, respectively [9].

Experimental Protocols for LSER Applications

Protocol 1: Determining Solute Descriptors

Principle: This protocol outlines the experimental and computational methods for determining the six Abraham solute descriptors (E, S, A, B, V, L) for new chemical compounds.

Materials and Reagents:

• High-purity solvents (n-hexane, n-hexadecane, water, octanol)
• Gas chromatograph with flame ionization detector
• HPLC system with appropriate columns
• Partition coefficient measurement apparatus
• Computational chemistry software (for preliminary estimates)

Procedure:

• Determine McGowan's Characteristic Volume (V_x): Calculate using molecular structure and atomic contributions according to the method described by McGowan.

• Measure Gas-Hexadecane Partition Coefficient (L):

  • Determine the gas-to-n-hexadecane partition coefficient at 298 K using inverse gas chromatography [9].
  • Use n-hexadecane as the stationary phase and measure retention times for the solute.
  • Calculate L from the retention data using standard thermodynamic relationships.

• Determine Excess Molar Refraction (E):

  • Measure the solute's refractive index at 293 K using a refractometer.
  • Calculate E using the established relationship between refractive index and electron polarizability [10].

• Measure Hydrogen Bond Acidity and Basicity (A and B):

  • Determine the solute's partition coefficients in multiple solvent systems with known LSER coefficients.
  • Use water-solvent and other complementary partition systems.
  • Solve the system of LSER equations to obtain A and B values [9] [10].

• Determine Dipolarity/Polarizability (S):

  • Calculate S from the determined L, E, A, B, and V values and measured partition coefficients using the LSER equation.
  • Alternatively, use computational approaches to estimate S based on molecular structure.

• Validate Descriptors:

  • Confirm the determined descriptors by predicting partition coefficients in additional solvent systems not used in the determination.
  • Compare predicted versus experimental values to ensure consistency.

Troubleshooting Tips:

• If inconsistent results are obtained, verify the purity of all solvents and compounds.
• Ensure all measurements are conducted at constant temperature (298 K).
• For compounds with limited solubility, consider using more sensitive analytical techniques.

Protocol 2: Applying LSER for Solubility Prediction

Principle: This protocol describes how to use established LSER equations and parameters to predict solute partitioning and solubility in pharmaceutical development contexts.

Materials and Reagents:

• Database of solute descriptors (e.g., Abraham LSER database)
• System coefficients for target solvents/phases
• Computational resources for calculations
• Validation standards with known partition behavior

Procedure:

• Define the System:
  • Identify the specific phase transfer or partition process of interest (e.g., water-to-membrane, blood-to-tissue).
  • Select the appropriate LSER equation based on the system [9].

• Compile Solute Descriptors:

  • Obtain the six Abraham descriptors (E, S, A, B, V, L) for the target solute from experimental measurements or reliable databases.
  • For new compounds, use group contribution methods to estimate descriptors [11].

• Identify System Coefficients:

  • Obtain the system-specific coefficients (e, s, a, b, v, l) for the target solvent system from literature or previous determinations.
  • Ensure the coefficients were determined using the same LSER form and descriptor scales.

• Calculate the Free Energy-Related Property:

  • Substitute the solute descriptors and system coefficients into the appropriate LSER equation.
  • Calculate the predicted partition coefficient or related property.

• Convert to Solubility Parameters (if needed):

  • Use the relationship between partition coefficients and activity coefficients.
  • Calculate the activity coefficient at infinite dilution from the partition coefficient.
  • Relate to solubility parameters using established thermodynamic relationships.

• Validate the Prediction:

  • Compare predictions with experimental data for similar compounds.
  • Assess the chemical reasonableness of the prediction based on molecular structure.

Troubleshooting Tips:

• If predictions seem inaccurate, verify the applicability domain of the system coefficients.
• Check for potential specific interactions not adequately captured by the LSER model.
• Consider using multiple LSER equations for the same prediction to assess consistency.

LSER Workflow and Relationship Mapping

LSER Application Workflow for Solubility Determination

Molecular Interactions in LSER Framework

Molecular Interactions Captured by LSER Model

Research Reagent Solutions for LSER Studies

Table 3: Essential Materials and Reagents for LSER Experimental Determination

Reagent/Material	Function in LSER Studies	Application Context
n-Hexadecane	Reference solvent for determining L descriptor	Gas-liquid partition measurements
Water (HPLC Grade)	Reference polar solvent for partition studies	Determination of A and B descriptors
1-Octanol	Model biological membrane solvent	Pharmaceutical partitioning studies
Inert Gas Chromatography Phases	Stationary phases for inverse GC	Measurement of gas-liquid partitions
Reference Compounds	Calibration standards with known descriptors	Method validation and standardization
Filter Papers/Substrates	Support media for liquid samples	Sample presentation for analysis

Advanced Applications in Drug Development

The LSER approach provides exceptional utility in pharmaceutical research by enabling quantitative prediction of solute distribution across biological barriers. For drug development professionals, LSER models can predict blood-brain barrier penetration, gastrointestinal absorption, and skin permeability based on molecular descriptors [9]. The model's ability to deconvolute the specific interactions governing solute partitioning allows medicinal chemists to rationally modify molecular structures to optimize distribution properties.

Recent advances have integrated LSER with equation-of-state thermodynamics through Partial Solvation Parameters (PSP), enhancing the extraction of thermodynamic information from LSER databases [9]. This integration allows researchers to estimate free energy changes upon hydrogen bond formation (ΔG_hb), as well as corresponding enthalpy (ΔH_hb) and entropy (ΔS_hb) contributions, providing deeper insight into the molecular interactions governing solubility behavior [9].

For solubility parameter determination research, LSER offers a pathway to quantify the relative contributions of different solubility parameter components (dispersion, polar, hydrogen bonding) from experimental partition data. This molecular-level understanding of interaction strengths facilitates more accurate predictions of solubility in complex pharmaceutical systems and supports the rational design of drug molecules with optimized solubility profiles.

Decoding the Six Key LSER Molecular Descriptors (Vx, E, S, A, B, L)

The Linear Solvation Energy Relationship (LSER) model, also known as the Abraham model, is a cornerstone predictive tool in environmental chemistry, pharmaceutical sciences, and chemical engineering for estimating solute partitioning and solubility parameters [9] [12]. This model's power lies in its ability to correlate a solute's free-energy-related properties with six fundamental molecular descriptors, providing a quantitative framework for understanding intermolecular interactions [9]. Within broader research on solubility parameter determination, LSER serves as a critical bridge between molecular structure and macroscopic thermodynamic behavior, enabling researchers to predict environmental fate, bioavailability, and physicochemical properties without extensive laboratory experimentation [13] [12]. The model operates through two primary linear equations that quantify solute transfer between phases, with the general form for transfer between condensed phases expressed as log(P) = cp + epE + spS + apA + bpB + vpVx, and for gas-to-solvent partitioning as log(KS) = ck + ekE + skS + akA + bkB + lkL [9].

The Six Key Molecular Descriptors

The LSER model characterizes solutes using six descriptors, each capturing a distinct aspect of molecular interaction potential. The following table summarizes these core descriptors and their physicochemical significance.

Table 1: The Six Key LSER Molecular Descriptors and Their Interpretations

Descriptor	Full Name	Molecular Property Represented	Interaction Type
Vx	McGowan's Characteristic Volume	Molecular size and volume [12]	Dispersion (van der Waals) interactions [9]
E	Excess Molar Refraction	Polarizability from π- and n-electrons [13] [12]	Dispersion interactions [9]
S	Dipolarity/Polarizability	Overall polarity and ability to stabilize a charge [12]	Dipole-dipole and dipole-induced dipole interactions [9]
A	Solute H-Bond Acidity	Ability to donate a hydrogen bond [12]	Specific hydrogen-bonding (acid-base) interactions [9]
B	Solute H-Bond Basicity	Ability to accept a hydrogen bond [12]	Specific hydrogen-bonding (acid-base) interactions [9]
L	Logarithm of Hexadecane-Air Partition Coefficient	General dispersion and polar interactions [13]	Various intermolecular interactions [9]

Detailed Descriptor Analysis

• V_x (McGowan's Characteristic Volume): This descriptor quantifies the molecular volume and is directly related to the energy cost of forming a cavity in the solvent to accommodate the solute. Larger V_x values typically lead to greater partitioning into organic phases due to enhanced dispersion interactions [12].

• E (Excess Molar Refraction): E reflects the solute's polarizability, particularly from Ï€-electrons and non-bonding orbitals. It is derived from refractive index data and indicates a molecule's ability to participate in non-specific polarization interactions. Aromatic compounds and molecules with conjugated systems typically exhibit higher E values [13] [12].

• S (Dipolarity/Polarizability): This descriptor represents the solute's ability to engage in dipole-dipole and dipole-induced dipole interactions. It encompasses both the permanent dipole moment and the molecular polarizability, playing a crucial role in partitioning into polar solvents [12].

• A and B (Hydrogen-Bonding Parameters): These complementary descriptors quantify the solute's hydrogen-bonding capacity. A (H-Bond Acidity) measures the solute's ability to donate a proton (hydrogen bond donor strength), while B (H-Bond Basicity) measures its ability to accept a proton (hydrogen bond acceptor strength). These are among the most important descriptors for predicting solubility in aqueous and hydrogen-bonding environments [12].

• L (Logarithm of Hexadecane-Air Partition Coefficient): Originally determined experimentally using n-hexadecane as a reference solvent, this descriptor encapsulates the solute's general affinity for condensed phases versus the gas phase. It reflects the overall combination of dispersion and polar interactions [13].

Experimental Protocols for Descriptor Determination

Traditional Experimental Determination

The following workflow outlines the multi-step process for empirically determining LSER molecular descriptors through laboratory measurements.

Figure 1: Experimental workflow for determining LSER descriptors.

Protocol 1: Experimental Determination of LSER Descriptors

Principle: Each descriptor is determined by measuring partition coefficients in multiple well-characterized solvent systems with known LSER coefficients, then solving the resulting system of equations [9].

Materials:

• Analytical balance (±0.0001 g precision)
• HPLC system with UV/RI detectors
• Gas chromatograph with FID detector
• Thermostated water baths (±0.1°C)
• n-Hexadecane, n-octanol, and other reference solvents of HPLC grade
• Hermetically sealed vials for partitioning experiments

Step-by-Step Procedure:

• Partition Coefficient Measurement:

  • Prepare solute solutions at multiple concentrations in relevant phases (e.g., water, n-octanol, n-hexadecane, air).
  • For liquid-liquid partitioning, equilibrate solute between n-octanol and water phases for 24 hours with constant shaking at 25°C.
  • Separate phases by centrifugation at 3000 rpm for 15 minutes.
  • Quantify solute concentration in each phase using HPLC or GC analysis.
  • Calculate partition coefficient as P = Corganic/Cwater.

• Data Collection Across Systems:

  • Measure partition coefficients for at least 6-10 different solvent systems with known LSER coefficients [9].
  • Include systems sensitive to different interaction types (e.g., hydrogen bonding, dispersion).

• Multilinear Regression Analysis:

  • Apply the general LSER equation: log(P) = c + eE + sS + aA + bB + vV_x
  • Use matrix algebra to solve for the six unknown descriptors (E, S, A, B, V, L).
  • Verify solution stability through statistical measures (e.g., correlation coefficients, residual analysis).

• Validation:

  • Test derived descriptor set by predicting partition coefficients in additional solvent systems not used in the regression.
  • Compare predicted versus experimental values to assess descriptor accuracy.

In Silico Determination Protocol

Protocol 2: Computational Determination of LSER Descriptors

Principle: Molecular descriptors are calculated using quantum chemical methods and Quantitative Structure-Property Relationship (QSPR) models, eliminating the need for extensive laboratory measurements [13].

Materials:

• Quantum chemical software (e.g., Gaussian, ORCA, or other DFT packages)
• Computer with sufficient computational resources (multi-core processor, 16+ GB RAM)
• Molecular modeling and visualization software
• LSER database for QSPR model development [12]

Step-by-Step Procedure:

• Molecular Geometry Optimization:

  • Build initial molecular structure using chemical drawing software or coordinate generation.
  • Perform geometry optimization using Density Functional Theory (DFT) with appropriate basis sets (e.g., B3LYP/6-311G).
  • Verify optimization convergence and confirm structure corresponds to energy minimum through frequency calculation.

• Electronic Property Calculation:

  • Compute molecular electrostatic potential surfaces and electron density distributions.
  • Calculate molecular volume using COSMO-RS or similar continuum solvation models [12].
  • Derive polarizability parameters from frequency calculations.

• Descriptor Calculation:

  • Calculate excess molar refraction (E) from computed polarizabilities [13].
  • Determine McGowan's characteristic volume (V_x) from the optimized molecular structure [12].
  • Compute hexadecane/air partition coefficient (L) using DFT-calculated properties [13].
  • Predict dipolarity/polarizability (S), solute H-bond acidity (A), and basicity (B) parameters using validated QSPR models developed with theoretical molecular descriptors [13].

• Validation of Computational Approach:

  • Compare computationally derived descriptors with available experimental values for reference compounds.
  • Assess predictive capability by constructing new LSER models for physicochemical properties and comparing performance with conventional LSER models [13].

Application in Solubility Parameter Determination

The relationship between LSER descriptors and solubility parameters provides powerful insights for pharmaceutical and environmental applications. The following diagram illustrates how molecular descriptors inform Hansen solubility parameters.

Figure 2: From LSER descriptors to solubility parameters and applications.

Protocol 3: Estimating Solubility Parameters from LSER Descriptors

Principle: LSER descriptors can be correlated with Hansen solubility parameters (δd, δp, δh) through mathematical relationships derived from solvation thermodynamics [9].

Materials:

• Set of LSER descriptors for target compound (experimentally or computationally derived)
• Mathematical software (Python, R, or MATLAB)
• Reference database of solubility parameters for validation

Step-by-Step Procedure:

• Establish Descriptor-Solubility Parameter Correlations:

  • Collect LSER descriptors and experimental solubility parameters for reference compounds.
  • Develop correlation equations using multilinear regression:
    • δd = f(V_x, E, L)
    • δp = f(S)
    • δh = f(A, B)

• Calculate Partial Solvation Parameters (PSP):

  • Utilize the equation-of-state thermodynamic framework to extract hydrogen-bonding information [9].
  • Compute hydrogen-bonding PSPs (σa and σb) from A and B descriptors [9].
  • Calculate dispersion PSP (σd) from V_x and E descriptors [9].
  • Determine polar PSP (σp) from S descriptor [9].

• Convert PSP to Solubility Parameters:

  • Transform PSP values to Hansen solubility parameters using established conversion factors.
  • Validate calculated solubility parameters against experimental data when available.

• Application to Solvent Selection:

  • Use calculated solubility parameters to predict compatibility with potential solvents.
  • Apply Hansen solubility sphere concept to identify optimal solvent systems for extraction, crystallization, or formulation.

Advanced Computational Integration

Recent advances have enabled more sophisticated integration of LSER with computational thermodynamics:

Quantum Chemical LSER (QC-LSER):

• New molecular descriptors derived from molecular surface charge distributions obtained from COSMO-type quantum chemical calculations [12].
• Thermodynamically consistent reformulation of LSER models allowing more accurate prediction of hydrogen-bonding free energies, enthalpies, and entropies [12].
• Ability to account for conformational changes during solvation through detailed quantum mechanical calculations [12].

Equation-of-State Integration:

• LSER descriptors inform equation-of-state models like SAFT and NRHB through Partial Solvation Parameters [9].
• Enables prediction of activity coefficients at infinite dilution (γ∞) through the relationship: ΔG12/RT = ln(φ10P10Vm2γ∞1/2/RT) [12].
• Enables extension of LSER predictions to varied temperature and pressure conditions beyond standard states [9].

Table 2: Key Research Reagents and Computational Resources for LSER Studies

Resource Category	Specific Examples	Function in LSER Research
Reference Solvents	n-Hexadecane, n-Octanol, Water, Diethyl Ether, Chloroform, Ethyl Acetate	Provide standardized systems for experimental determination of partition coefficients and descriptor validation [9].
Analytical Instruments	HPLC-UV, GC-FID, Headspace Samplers, Spectrophotometers	Precisely quantify solute concentrations in multiphase systems for partition coefficient measurement.
Computational Software	Gaussian, ORCA, COSMO-RS, OpenQSAR	Perform quantum chemical calculations, derive molecular descriptors, and build predictive models [12].
LSER Databases	Abraham LSER Database, UFZ-LSER Database	Provide curated experimental descriptor values for model development and validation [12].
QSPR Tools	DRAGON, PaDEL-Descriptor, RDKit	Calculate molecular descriptors for in silico LSER parameter estimation [13].

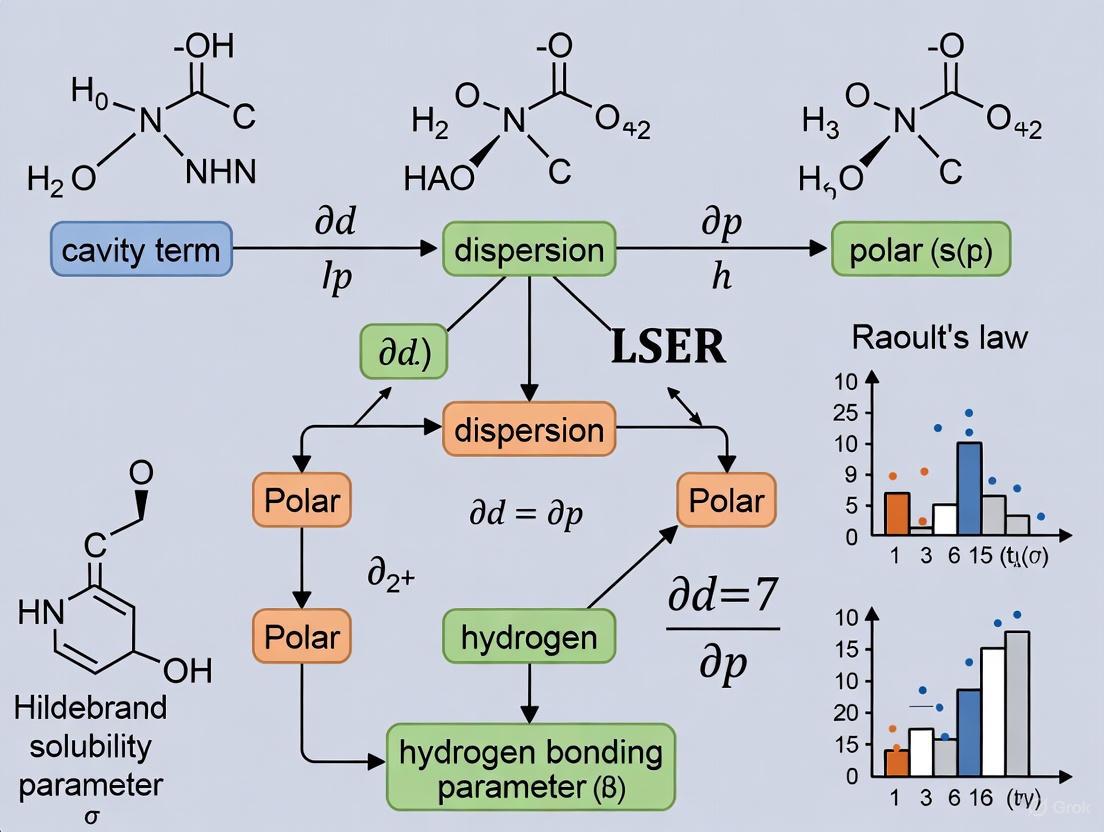
The Thermodynamic Basis of LSER Linearity and Solute-Solvent Interactions

The Linear Solvation Energy Relationship (LSER) model, particularly in the form of the Abraham solvation parameter model, stands as one of the most successful predictive tools for understanding a broad variety of chemical, biomedical, and environmental processes [9]. The model is celebrated for its ability to correlate and predict free-energy-related properties of solutes based on a set of molecular descriptors. Its robustness stems from a sound thermodynamic basis and the wise selection of molecular descriptors that comprehensively characterize each solute molecule [14]. The wealth of thermodynamic information contained within the freely accessible LSER database is of immense value for applications ranging from solvent screening in pharmaceutical development to predicting environmental fate of chemicals [9].

The core of the LSER model lies in its linear free energy relationships (LFER), which quantify the transfer of a solute between two phases. The remarkable feature of these relationships is their observed linearity, even for strong, specific interactions like hydrogen bonding. This application note delves into the thermodynamic basis of this linearity, provides protocols for its practical application, and illustrates how it can be integrated with modern computational and experimental approaches for solubility parameter determination within a research thesis framework [9] [14].

Theoretical Foundation: Thermodynamic Basis of LSER Linearity

The LSER Equations and Molecular Descriptors

The LSER model utilizes two primary equations to quantify solute transfer. The first describes partitioning between two condensed phases [9] [14]: log (P) = cp + epE + spS + apA + bpB + vpVx [9]

The second equation describes gas-to-condensed phase partitioning [9] [14]: log (KS) = ck + ekE + skS + akA + bkB + lkL [9]

In these equations, the upper-case letters represent solute-specific molecular descriptors, while the lower-case letters are the complementary system- or solvent-specific coefficients obtained through multilinear regression of experimental data [9] [14].

Table 1: LSER Solute Molecular Descriptors and Their Physico-Chemical Interpretation

Descriptor	Symbol	Physico-Chemical Interpretation
McGowan's Characteristic Volume	Vx	Related to the size of the solute molecule and the energy required to form a cavity in the solvent [14].
Gas-Hexadecane Partition Coefficient	L	Describes the solute's ability to participate in dispersive van der Waals interactions [9] [14].
Excess Molar Refraction	E	Measures the solute's polarizability due to π- and n-electrons [10].
Dipolarity/Polarizability	S	Reflects the solute's ability to engage in dipole-dipole and dipole-induced dipole interactions [10].
Hydrogen Bond Acidity	A	Quantifies the solute's ability to donate a hydrogen bond [10] [14].
Hydrogen Bond Basicity	B	Quantifies the solute's ability to accept a hydrogen bond [10] [14].

Provenance of Linearity in LSER Models

The linearity observed in LSER equations, even for specific interactions like hydrogen bonding, has a firm grounding in solution thermodynamics. The process of solvation or partitioning can be conceptually broken down into two primary steps [10]:

• An endoergic process involving cavity formation within the solvent and solvent reorganization.
• An exoergic process driven by attractive solute-solvent interactions.

The LSER model successfully parameterizes the Gibbs free energy change of this overall process. The product terms in the LSER equations (e.g., aA, bB) represent the contributions of specific intermolecular interactions to the total free energy. The linearity holds because, for a given phase transfer process and within a congeneric set of solutes, the free energy contribution from each type of interaction is approximately additive [9].

Research combining equation-of-state solvation thermodynamics with the statistical thermodynamics of hydrogen bonding has verified the thermodynamic basis of LFER linearity. It has been shown that the model effectively captures the balance between the different interaction energies and entropic contributions, justifying the simple linear form of the relationships [9]. The coefficients (e.g., a and b) are system descriptors that reflect the solvent's complementary ability to participate in that specific interaction (e.g., basicity and acidity, respectively) [9] [14].

Experimental Protocols for LSER and Solubility Determination

Protocol 1: Determining Solute LSER Molecular Descriptors

Principle: This protocol outlines the standard procedure for obtaining the six Abraham LSER descriptors (E, S, A, B, V, L) for a new solute molecule. These descriptors are foundational for any subsequent LSER analysis.

Materials:

• Solute of interest (high purity)
• Solvents: n-Hexadecane, water, and other well-characterized solvents from the LSER database
• Gas Chromatograph (GC) equipped with a flame ionization detector (FID)
• High-Performance Liquid Chromatograph (HPLC) system with a UV/Vis detector
• Partitioning vessels (e.g., shake-flasks)
• Constant-temperature incubator shaker
• Analytical balance

Procedure:

• McGowan Volume (Vx): Calculate Vx using a group contribution method based on the molecular structure of the solute. This is a computational determination and does not require experimentation [14].
• Excess Molar Refraction (E): Determine the solute's refractive index experimentally and calculate E using the Lorentz-Lorenz equation. This value is indicative of the solute's polarizability [10].
• Gas-Hexadecane Partition Coefficient (L): a. Using gas chromatography, measure the retention time of the solute on a non-polar column (e.g., polydimethylsiloxane) with n-hexadecane as the stationary phase. b. Relate the retention time to the partition coefficient L at 298 K using known standards [9] [14].
• Hydrogen Bond Acidity (A) and Basicity (B): a. Measure the solute's partition coefficient in several well-characterized solvent/water or solvent/gas systems (e.g., octanol-water, ether-water) using the shake-flask method. b. In a sealed vessel, dissolve a known amount of solute in a mixture of two immiscible solvents (e.g., water and octanol). c. Agree vigorously in a constant-temperature incubator shaker (e.g., 25°C) for 24-48 hours to reach equilibrium. d. Allow phases to separate, then sample each phase and quantify the solute concentration using HPLC-UV/Vis. e. The partition coefficient is the ratio of concentrations in the two phases.
• Dipolarity/Polarizability (S): This descriptor is typically determined indirectly by multilinear regression analysis of the partition coefficient data obtained in step 4, along with the other known descriptors (E, Vx, A, B, L).

Data Analysis: The final set of descriptors is obtained by fitting a large set of experimentally determined partition coefficients (log P) across multiple solvent systems to the LSER equation. The values are refined iteratively until a consistent set of six descriptors is obtained that best predicts all the experimental data. These descriptors can then be added to the LSER database for future use [9] [10].

Protocol 2: Measuring Solubility for Hansen Parameter Determination

Principle: The static gravimetric (shake-flask) method is a reliable technique for determining equilibrium solubility, which is crucial for calibrating and validating solubility parameters, such as Hansen Solubility Parameters (HSP) [15] [16].

Materials:

• Solute of interest (e.g., a drug molecule like Naproxen or 17-α hydroxyprogesterone)
• Pure solvents and solvent mixtures of varying polarity and hydrogen-bonding capability (e.g., methanol, ethanol, acetone, ethyl acetate, water, DMF)
• Jacketed vessels connected to a thermostatted water bath
• Laboratory incubator-shaker
• Centrifuge
• UV/Vis Spectrophotometer or HPLC for concentration analysis
• Analytical balance (precision ± 0.1 mg)
• Micropipettes

Procedure:

• Preparation: Pre-saturate all solvents by adding a small excess of solute and agitating for several hours prior to the main experiment.
• Equilibration: a. Weigh an excess amount of solute into a series of jacketed vessels. b. Add a known mass of pre-saturated solvent to each vessel. c. Seal the vessels and maintain them at a constant temperature (e.g., 298.15 K) using a circulating water bath. d. Agitate the suspensions continuously using a magnetic stirrer or place them in an incubator-shaker for a sufficient period (typically 24-72 hours) to ensure solid-liquid equilibrium is reached.
• Sampling: a. After equilibration, stop agitation and allow the undissolved solute to settle. b. To prevent precipitation, maintain the sampling temperature. Withdraw an aliquot of the saturated supernatant. For suspensions that are slow to settle, use a pre-warmed centrifuge to separate the solid. c. Carefully filter the supernatant if necessary using a pre-warmed syringe filter.
• Analysis: a. Dilute the saturated solution as needed with a suitable solvent (e.g., 50% ethanol for UV analysis). b. Quantify the solute concentration using a pre-calibrated method: * UV/Vis Spectrophotometry: Measure absorbance at the solute's λmax and compare to a calibration curve [15] [16]. * HPLC: Use for higher specificity, especially in complex solvent mixtures [16].
• Repeat: Repeat the procedure at different temperatures to study the temperature dependence of solubility.

Data Analysis: The molar solubility is calculated from the concentration, molar mass, and density of the solution. The experimental solubility data in multiple solvents can be used to determine the Hansen Solubility Parameters (δD, δP, δH) of the solute by finding the center of the "solubility sphere" in three-dimensional parameter space [17] [18].

Data Presentation and Modeling

Quantitative Data from LSER and Solubility Studies

Table 2: Experimentally Determined Solubility (x₁) of 17-α Hydroxyprogesterone in Selected Pure Solvents at 298.15 K [15]

Solvent	HSP δD (MPa¹/²)	HSP δP (MPa¹/²)	HSP δH (MPa¹/²)	Solubility x₁ (10³ mol·mol⁻¹)
Methanol	15.3 [18]	12.4 [18]	22.5 [18]	1.210
Ethanol	16.1 [18]	5.8 [18]	15.9 [18]	1.788
Acetone	15.7 [18]	10.5 [18]	7.0 [18]	Data not available in source
Ethyl Acetate	16.1 [18]	5.8 [18]	5.2 [18]	Data not available in source
Tetrahydrofuran	16.9 [18]	5.8 [18]	8.1 [18]	Data not available in source
N,N-Dimethylformamide (DMF)	18.6 [18]	16.5 [18]	10.3 [18]	0.06548 (at 323.15 K)

Table 3: Representative LSER System Coefficients (lf) for Gas-to-Solvent Partitioning (log Ks) [9] [14]

System Coefficient	Chemical Interpretation	Example Value for a Polar Solvent
l	Resilience of the solvent to separate molecules and create a cavity for the solute.	Positive value
e	Solvent's ability to engage in polarization interactions with the solute.	Positive value
s	Solvent's complementary dipolarity/polarizability.	Positive value
a	Solvent's hydrogen-bond basicity (complementary to solute acidity A).	Positive value
b	Solvent's hydrogen-bond acidity (complementary to solute basicity B).	Positive value

Thermodynamic Modeling of Solubility Data

Experimental solubility data can be correlated and interpreted using various thermodynamic models. The modified Apelblat model is widely used for its accuracy in describing the temperature dependence of solubility [15]: ln x = A + B/T + C ln T Where x is the mole fraction solubility, T is the absolute temperature, and A, B, C are empirical parameters.

Furthermore, the van't Hoff analysis allows for the calculation of thermodynamic dissolution parameters [15] [16]: ln x = - (ΔsolH° / R)(1/T) + (ΔsolS° / R) Where ΔsolH° is the standard dissolution enthalpy, ΔsolS° is the standard dissolution entropy, and R is the gas constant. A positive ΔsolH° indicates an endothermic dissolution process, which is common for many organic solutes in organic solvents [15].

Visualization of Concepts and Workflows

Diagram 1: Integrated research workflow for combining LSER and solubility parameter studies.

The Scientist's Toolkit: Essential Research Reagents and Materials

Table 4: Key Research Reagents and Computational Tools for LSER and Solubility Studies

Item / Solution	Function / Purpose
n-Hexadecane	Standard solvent for determining the gas-liquid partition coefficient (L) descriptor [9] [14].
1-Octanol / Water System	Benchmark biphasic system for measuring partition coefficients (log P) used to refine A, B, and S descriptors [10].
Solvent Library	A diverse set of solvents covering a wide range of polarity, polarizability, and hydrogen-bonding characteristics (e.g., alkanes, ethers, ketones, alcohols, DMSO) for comprehensive solubility profiling and LSER coefficient determination [9] [15].
Abraham LSER Database	A freely accessible, comprehensive database containing pre-determined LSER molecular descriptors for thousands of solutes and system coefficients for numerous solvents/phases. It is the primary resource for initial predictions and comparisons [9] [14].
COSMO-RS / COSMOtherm	A quantum mechanics-based a priori predictive method for solvation thermodynamics. Used to predict solvation properties and can be interconnected with LSER to provide insights and estimates, especially for new molecules [9] [14].
Machine Learning Libraries (e.g., for CatBoost, ANN)	Advanced data-driven frameworks used to develop predictive models for properties like solubility parameters, capturing complex, non-linear relationships from large datasets [19].
Tyrosine kinase-IN-6	Tyrosine kinase-IN-6, MF:C37H31F2N5O5S, MW:695.7 g/mol
KRPpSQRHGSKY-NH2	KRPpSQRHGSKY-NH2, MF:C57H96N23O18P, MW:1422.5 g/mol

Linking LSER Descriptors to Partial Solvation Parameters (PSP)

Within the broader context of developing robust Linear Solvation Energy Relationship (LSER) models for solubility parameter determination, the Partial Solvation Parameter (PSP) approach emerges as a powerful, thermodynamically grounded framework. It effectively interconnects diverse Quantitative Structure-Property Relationship (QSPR)-type databases and molecular descriptors, facilitating a unified approach to predicting solvation phenomena [9] [20]. While traditional models like the Hansen Solubility Parameter (HSP) and Abraham's LSER have been widely used in pharmaceutics and material science, the PSP approach offers a distinct advantage by providing a coherent thermodynamic model for both bulk phases and interfaces, allowing for the direct calculation of free energy changes upon molecular interactions [21] [20]. This application note details the formalisms, protocols, and practical applications for linking established LSER molecular descriptors to the PSP framework, providing researchers and drug development professionals with a method to leverage existing LSER data for advanced thermodynamic modeling.

Theoretical Foundation and Definitions

The PSP framework deconstructs a molecule's solvation behavior into four complementary parameters, each mapping to specific intermolecular interactions quantified by LSER descriptors [20]. The core definitions establishing the one-to-one correspondence between LSER descriptors and PSPs are summarized in the table below.

Table 1: Fundamental Relationships between LSER Descriptors and Partial Solvation Parameters

Partial Solvation Parameter (PSP)	LSER Descriptor Mapping	Physical Interaction Represented
Dispersion PSP (σd)	σd = 100 * (3.1 * Vx + E) / Vm [20]	Hydrophobicity, cavity effects, and dispersion/weak non-polar interactions. Maps McGowan volume (Vx) and excess refractivity (E).
Polarity PSP (σp)	σp = 100 * S / Vm [20]	Dipolar interactions (Debye and Keesom types). Maps the dipolarity/polarizability descriptor (S).
Acidity PSP (σGa)	σGa = 100 * A / Vm [20]	Hydrogen-bond donating (acidic) character. A Gibbs free-energy descriptor. Maps the hydrogen bond acidity descriptor (A).
Basicity PSP (σGb)	σGb = 100 * B / Vm [20]	Hydrogen-bond accepting (basic) character. A Gibbs free-energy descriptor. Maps the hydrogen bond basicity descriptor (B).

A key thermodynamic advantage of the PSP framework is its ability to directly calculate the Gibbs free energy change (G_HB) upon the formation of a hydrogen bond (or Lewis acid-base interaction) using the acidity and basicity PSPs [20]: -G_HB = 2 * Vm * σGa * σGb = 20000 * A * B (at 298 K) [20].

This free energy change can be further decomposed into enthalpy (E_HB) and entropy (S_HB) contributions using the derived working equations [20]: E_HB = -30,450 * A * B S_HB = -35.1 * A * B

The following diagram illustrates the logical workflow for extracting thermodynamic information from LSER descriptors via the PSP framework.

Experimental and Computational Protocols

Protocol 1: Determination of LSER Descriptors for PSP Calculation

For compounds where LSER descriptors are not available in databases, they can be determined experimentally via chromatographic methods.

• Objective: To experimentally determine the solute-specific LSER descriptors (A, B, S) required for PSP calculation.
• Materials and Reagents:
  • Analytical HPLC System: Configured with multiple detection modes (e.g., DAD, RID).
  • Stationary Phases: A system of eight reversed-phase, normal-phase, and hydrophilic interaction (HILIC) HPLC columns to probe diverse interactions [22].
  • Mobile Phases: Solvents of varying polarity and hydrogen-bonding character (e.g., water, acetonitrile, methanol, alkanes).
  • Test Solutes: The compounds of interest (e.g., pharmaceuticals, pesticides).
  • Reference Compounds: A set of standards with known LSER descriptors for column calibration.
• Procedure:
  • Column Calibration: Separately inject a set of reference compounds with known LSER descriptors onto each of the eight HPLC columns. For each reference compound, measure the retention factor (log k).
  • Multiple Linear Regression: For each column, perform a multiple linear regression to establish a system-specific equation: log k = c + eE + sS + aA + bB + vVx [22]. This determines the system constants (e, s, a, b, v) for that column.
  • Analyze Target Solutes: Inject the target solutes onto each calibrated HPLC column and record their retention factors.
  • Descriptor Determination: Using the measured retention factors (log k) across the multiple chromatographic systems and the known system constants, perform a multi-variable regression analysis to solve for the solute's descriptors (E, S, A, B, Vx). The McGowan volume (Vx) can often be calculated from molecular structure prior to this step [20].
• Notes: This protocol is particularly suited for complex, multifunctional compounds like pharmaceuticals and pesticides, which often have A, S, and B values at the upper end of the known numerical range [22].

Protocol 2: Computational Calculation of PSPs from LSER Descriptors

Once the LSER descriptors are known, either from databases or experimental determination, the PSPs can be calculated directly.

• Objective: To calculate the full set of Partial Solvation Parameters from a compound's known LSER descriptors and molar volume.
• Prerequisites:
  • LSER Descriptors: A, B, S, E, Vx for the target compound.
  • Molar Volume (Vm): The molar volume of the compound at the temperature of interest.
• Computational Procedure:
  • Calculate Dispersion PSP (σd): Apply the formula σd = 100 * (3.1 * Vx + E) / Vm [20].
  • Calculate Polarity PSP (σp): Apply the formula σp = 100 * S / Vm [20].
  • Calculate Acidity PSP (σGa): Apply the formula σGa = 100 * A / Vm [20].
  • Calculate Basicity PSP (σGb): Apply the formula σGb = 100 * B / Vm [20].
• Data Analysis:
  • The calculated PSPs can be used to estimate the cohesive energy density (ced) contribution from hydrogen bonding: ced_HB = - (r1 * ν11 * E_HB) / Vm, where r1 is the number of molecular segments, and ν11 is the number of hydrogen bonds per mole [20].
  • The total solubility parameter can be approximated from the PSPs, acknowledging that ced_total ≈ σd² + σp² + σGa² + σGb² [21].

The Scientist's Toolkit: Key Reagents and Materials

Table 2: Essential Research Reagents and Materials for LSER-PSP Studies

Item	Function / Application	Relevant Protocol
Multi-Chemistry HPLC Column Set	Set of 8 reversed-phase, normal-phase, and HILIC columns for comprehensive profiling of solute interactions with different stationary phases.	Protocol 1 [22]
Reference Compound Library	A curated set of chemical standards with pre-established, reliable LSER descriptors. Used to calibrate chromatographic systems.	Protocol 1 [22]
Inverse Gas Chromatography (IGC)	An alternative technique to determine PSPs/LSER descriptors of solid materials (e.g., APIs, polymers) by using probe gases.	Cited in [20]
COSMO-RS Software & Database	Quantum chemistry-based thermodynamic model and database (e.g., COSMObase) used for in-silico estimation of PSPs and σ-profiles.	Cited in [21] [20]
Abraham LSER Database	A freely accessible database containing a large inventory of experimentally derived LSER descriptors for numerous compounds.	Cited in [9] [20]
Neuraminidase-IN-19	Neuraminidase-IN-19|Potent Influenza NA Inhibitor	Neuraminidase-IN-19 is a potent influenza virus neuraminidase inhibitor for antiviral research. This product is For Research Use Only. Not for human or veterinary diagnostic or therapeutic use.
Steroid sulfatase-IN-7	Steroid sulfatase-IN-7, MF:C20H17F3N2O5S, MW:454.4 g/mol	Chemical Reagent

Data Presentation and Application in Pharmaceuticals

The utility of the LSER-PSP linkage is demonstrated by its application in predicting critical properties. The following table showcases calculated hydrogen-bond thermodynamics for hypothetical molecular pairs, derived directly from their A and B descriptors [20].

Table 3: Calculated Hydrogen-Bond Thermodynamics from LSER Descriptors (at 298 K)

Acid-Base Pair Interaction	A (Acid) * B (Base)	G_HB (J/mol)	E_HB (J/mol)	S_HB (J/(mol·K))
Weak Interaction	0.1	-2,000	-3,045	-3.51
Moderate Interaction	0.3	-6,000	-9,135	-10.53
Strong Interaction	0.6	-12,000	-18,270	-21.06

This framework has been successfully applied to predict activity coefficients at infinite dilution, octanol/water partition coefficients, and the miscibility of pharmaceuticals in various solvents [21] [20]. For instance, in drug development, PSPs calculated via this method have proven helpful in predicting drug solubility in various solvents and in calculating the different contributions to surface energy, which is critical for formulation design [20]. The ability to convert PSPs back to classical solubility parameters or LSER values creates a unified, versatile tool for pharmaceutical scientists [20].

Concluding Remarks

The formalized linkage between LSER descriptors and Partial Solvation parameters provides a robust, thermodynamically sound pathway for enriching solubility prediction models. By bridging the gap between a widely used empirical database (LSER) and an equation-of-state-based framework (PSP), researchers can extract profound thermodynamic insights—such as the free energy, enthalpy, and entropy of hydrogen bonding—from readily available molecular descriptors. This integration enhances the predictive power for complex phenomena like solute partitioning and miscibility, offering a more nuanced and effective tool for applications ranging from solvent selection in drug formulation to the design of novel polymeric materials.

Implementing LSER Models: From Theory to Pharmaceutical Practice

Linear Solvation Energy Relationships (LSER) represent a pivotal quantitative approach for predicting solvation-related properties, crucially applied within pharmaceutical research to address the pervasive challenge of poor drug solubility. The LSER model quantitatively correlates the free-energy-related properties of a solute to a set of molecular descriptors that encode specific intermolecular interaction capabilities [9]. For researchers and drug development professionals, a robust LSER model provides an indispensable tool for solvent screening, crystallization process optimization, and guiding drug dosage form design, thereby directly enhancing drug production efficiency and clinical applicability [23]. This protocol details a comprehensive, step-by-step methodology for constructing, validating, and applying a thermodynamically grounded LSER model, with a particular emphasis on solubility parameter determination for active pharmaceutical ingredients (APIs).

Theoretical Framework of LSER

The foundational principle of LSER is that a free-energy-related property (log P) of a solute can be expressed as a linear combination of its molecular descriptors and the complementary system coefficients [9]. The two primary equations used for solute transfer between phases are:

For partitioning between two condensed phases (e.g., water-to-organic solvent): log (P) = câ‚š + eâ‚šE + sâ‚šS + aâ‚šA + bâ‚šB + vâ‚šVâ‚“ [9]

For gas-to-organic solvent partitioning: log (Kâ‚›) = câ‚– + eâ‚–E + sâ‚–S + aâ‚–A + bâ‚–B + lâ‚–L [9]

Table: LSER Solute Molecular Descriptors

Descriptor	Symbol	Physical Interpretation
McGowan's Characteristic Volume	Vâ‚“	Represents the size of the solute molecule and encodes dispersion interactions [9].
Gas-Liquid Partition Coefficient	L	The logarithm of the gas-hexadecane partition coefficient, describing solute partitioning into a van der Waals solvent [9].
Excess Molar Refraction	E	Measures the solute's ability to interact via polarizability, often related to π- or n-electrons [9].
Dipolarity/Polarizability	S	Characterizes the solute's ability to engage in dipole-dipole and dipole-induced dipole interactions [9].
Hydrogen Bond Acidity	A	Quantifies the solute's ability to donate a hydrogen bond [9].
Hydrogen Bond Basicity	B	Quantifies the solute's ability to accept a hydrogen bond [9].

The lower-case coefficients (e.g., eâ‚š, sâ‚š, aâ‚š, bâ‚š, vâ‚š) in these equations are the system-specific constants, or LSER coefficients. They are considered solvent descriptors that embody the complementary effect of the solvent (or phase) on the solute-solvent interactions. These coefficients are typically determined via multiple linear regression against a dataset of experimental values for a wide range of solutes with known descriptors [9].

Experimental Determination of Solubility Data

The accuracy of any LSER model is contingent on the quality of the experimental solubility data used for its calibration. This section outlines a standardized protocol for obtaining reliable solubility measurements.

Materials and Equipment

Table: Essential Research Reagents and Equipment

Item Name	Function/Description
Analytical Balance	Precisely weighing the drug (API) and solvents.
Thermostatic Shaker Bath	Maintaining a constant temperature during the equilibration process.
HPLC System with Detector	Quantifying the concentration of the drug in the saturated solution (e.g., carprofen) [23].
UV-Vis Spectrophotometer	An alternative method for concentration determination of drugs with suitable chromophores [24].
Membrane Filters (e.g., 0.45 μm)	Removing undissolved solid particles from the saturated solution prior to analysis.
Differential Scanning Calorimeter (DSC)	Determining key thermal properties of the pure API, such as melting temperature (Tm) and enthalpy of fusion (ΔfusH) [23].
X-ray Powder Diffractometer (PXRD)	Verifying the solid-state form (polymorph) of the API before and after solubility experiments to ensure no crystal transformation occurred during dissolution [23].

Solubility Measurement Protocol: The Static Method

The following is a detailed protocol for measuring saturation solubility, adapted from the methodology successfully applied to carprofen [23].

• Preparation of Saturated Solutions: An excess amount of the solid drug (API) is added to a known volume of a pure or mixed solvent in a sealed vessel.
• Equilibration: The suspensions are placed in a thermostatic shaker bath. Equilibrium is achieved by agitating the suspensions at a constant temperature (e.g., between 288.15 K and 328.15 K) for a sufficient duration, typically at least 24 hours, to ensure that the solid phase is in equilibrium with the solution [23] [24].
• Sampling: After equilibration, the agitation is stopped to allow the undissolved solids to settle.
• Filtration and Dilution: An aliquot of the saturated supernatant is carefully withdrawn and filtered through a membrane filter to remove any fine particulate matter. The filtrate may be diluted with an appropriate solvent if necessary, to fall within the quantitative range of the analytical method.
• Concentration Analysis: The concentration of the drug in the filtered (and potentially diluted) solution is determined using a pre-calibrated analytical method, such as High-Performance Liquid Chromatography (HPLC) or UV-Vis spectrophotometry [23] [24].

Diagram 1: Experimental workflow for static solubility measurement.

Solid-State Characterization

To ensure the integrity of the solubility data, it is critical to verify that the solid phase of the API remains unchanged throughout the dissolution process.

• Pre-Experiment: Characterize the starting API material using PXRD and DSC.
• Post-Experiment: Recover the undissolved solid from the equilibrium slurry and subject it to PXRD analysis. Compare the diffraction patterns before and after the experiment. The absence of new peaks confirms no crystal transformation, solvate formation, or degradation occurred, thereby validating the solubility measurement [23].

Computational Implementation and Model Fitting

Assembling the Data Matrix

Construct a data matrix where each row represents a single solute-solvent system (or a single experimental condition) and each column represents a variable. The core data required includes:

• Dependent Variable (Y): The experimentally determined property (e.g., log S, log P).
• Independent Variables (X): The six solute-specific molecular descriptors (Vâ‚“, L, E, S, A, B) for each solute in the dataset.

Regression Analysis and Model Validation

The core computational workflow for building and validating the LSER model is as follows:

Diagram 2: Computational workflow for LSER model building and validation.

• Data Splitting: Divide the full dataset into a training set (e.g., 70-80%) for model calibration and a test set (e.g., 20-30%) for independent validation.
• Multiple Linear Regression (MLR): Use the training set to perform MLR, solving for the LSER coefficients (system constants) that minimize the difference between the experimental and predicted log P or log S values.
• Model Validation: Use the derived model to predict the properties of the solutes in the test set. Compare these predictions to the experimental values.
• Statistical Analysis: Evaluate the model's performance using statistical metrics [23]:
  • R² (Coefficient of Determination): Measures the proportion of variance in the dependent variable that is predictable from the independent variables. An R² > 0.9 typically indicates a strong model.
  • Root Mean Square Deviation (RMSD): Quantifies the average magnitude of the prediction errors.
  • Absolute Relative Deviation (ARD): Provides a relative measure of the error for individual data points.

Extraction of Thermodynamic Information

A significant advantage of the LSER framework is its foundation in free energy, which allows for the extraction of profound thermodynamic insights into the dissolution process. The relationship between the Gibbs free energy of solvation and the LSER model is direct: log Kâ‚› ∝ -ΔG_sol/RT. By analyzing the relative magnitudes of the LSER coefficients and their corresponding terms (e.g., aâ‚šA vs bâ‚šB), one can deconvolute the contributions of different interaction types (e.g., hydrogen bonding acidity/basicity vs. dispersion) to the overall solvation free energy [9].

Furthermore, by measuring solubility at multiple temperatures and applying van't Hoff analysis or correlating the data with models like the Apelblat equation, it is possible to extract apparent standard thermodynamic functions of dissolution [23]:

• Enthalpy (ΔH⁰_sol): Indicates whether the dissolution process is endothermic (ΔH⁰_sol > 0) or exothermic (ΔH⁰_sol < 0).
• Entropy (ΔS⁰_sol): Reflects changes in molecular order.
• Gibbs Free Energy (ΔG⁰_sol): Determines the overall spontaneity of the process.

The relative contribution of enthalpy (ξ_H) and entropy (ξ_S) to the Gibbs free energy can be calculated. For many APIs like carprofen, the dissolution process is endothermic and entropy-driven, meaning the entropy term (TΔS⁰_sol) is the dominant contributor to a negative ΔG⁰_sol at higher temperatures [23].

Application in Solubility Parameter Determination

The LSER model provides a powerful pathway for determining and interpreting the solubility parameters of APIs. The LSER solvent coefficients (eâ‚š, sâ‚š, aâ‚š, bâ‚š, vâ‚š) offer a quantitative profile of the solvent's interaction capabilities. A solvent that is optimal for dissolving a specific API will have a coefficient profile that closely matches the descriptor profile of the API. For instance, a high hydrogen bond basicity descriptor (B) in an API necessitates a solvent with a large hydrogen bond acidity coefficient (aâ‚š) for strong complementary interaction [23] [9].

This LSER analysis can be integrated with traditional solubility parameter theories, such as Hansen Solubility Parameters (HSPs). The LSER descriptors provide a more granular, chemically intuitive breakdown of the intermolecular forces that constitute the total solubility parameter. The S descriptor relates to the polar component (δ_P), while the A and B descriptors inform the hydrogen bonding component (δ_H). The Vâ‚“ and L descriptors are linked to the dispersion component (δ_D). Therefore, a robust LSER model does not just predict solubility; it explains it in terms of fundamental, quantitative molecular interactions, providing a solid basis for rational solvent selection in pharmaceutical process development [23].

The development of new chemical entities (NCEs) in the pharmaceutical industry faces a significant challenge: approximately 90% of these compounds exhibit poor water solubility, which severely limits their bioavailability and therapeutic potential [24]. Among innovative strategies to overcome this hurdle, supramolecular chemistry offers cucurbit[7]uril (CB[7]) as a powerful macrocyclic host capable of forming stable inclusion complexes with hydrophobic drugs [25]. This case study explores the application of Linear Solvation Energy Relationships (LSER) modeling to predict the solubilizing effect of CB[7] on poorly soluble Active Pharmaceutical Ingredients (APIs), providing researchers with a computational framework to prioritize experimental work.

CB[7] represents an exceptional molecular container with distinctive advantages over traditional excipients like cyclodextrins. Its structure features a hydrophobic cavity and polar carbonyl portals, enabling exceptionally high binding affinities (up to 10¹⁵ M⁻¹ in water) with various drug molecules [24]. Unlike cyclodextrins, CB[7] demonstrates remarkable stability across wide pH ranges, including strong acidic and weak alkaline conditions [24]. With moderate aqueous solubility (20-30 mM) and established biocompatibility profiles showing negligible systemic toxicity in vitro and in vivo, CB[7] presents an attractive platform for pharmaceutical formulation [25] [24].

The LSER model transforms the traditionally empirical process of excipient selection into a rational, prediction-driven approach. By quantifying molecular interactions between drugs, CB[7], and the aqueous environment, researchers can efficiently identify optimal candidate compounds for experimental validation, significantly accelerating pre-formulation stages.

Theoretical Background and LSER Model Development

LSER Fundamentals for Solubility Prediction

Linear Solvation Energy Relationships represent a well-established theoretical framework that correlates molecular descriptors with physicochemical properties. In pharmaceutical contexts, LSER models describe how structural features influence solubility, permeability, and other critical parameters. The general LSER equation for solubility takes the form:

log S = c + vD + eE + iL

where S represents solubility, D corresponds to molecular dimension descriptors, E encapsulates molecular interaction parameters, L reflects macroscopic properties, and c is a constant [24].

When adapted for predicting CB[7]-mediated solubility enhancement, the standard LSER model requires extension to account for the ternary complex system involving the drug, CB[7], and aqueous environment. The modified multi-parameter model incorporates specific descriptors capturing host-guest interactions and complex properties [26] [24].

Key Molecular Descriptors in CB[7]-Drug Solubilization

Research has identified five critical parameters governing drug solubilization by CB[7]:

• Surface area of inclusion complexes (A₃): Reflects the molecular footprint of the drug-CB[7] complex, influencing solvation energy [24]
• LUMO energy of inclusion complexes (E₃LUMO): Indicates the electron-accepting potential of the complex [24]
• Polarity index of inclusion complexes (I₃): Measures overall polarity changes upon complexation [24]
• Electronegativity of drugs (χ₁): Affects charge transfer interactions with CB[7] portals [24]
• Oil-water partition coefficient of drugs (log P₁w): Represents inherent drug hydrophobicity [24]

These parameters can be computationally derived using Density Functional Theory (DFT) calculations, providing a quantitative basis for solubility predictions without extensive experimental screening [26].

Computational Protocol: LSER Model Implementation

Density Functional Theory Calculations

Objective: To compute molecular descriptors for drugs and their CB[7] inclusion complexes.

Procedure:

• Molecular Optimization: Perform geometry optimization for each drug molecule and proposed CB[7]-drug complex using DFT methods (B3LYP/6-31G* level)
• Electronic Property Calculation: Calculate frontier molecular orbitals (HOMO/LUMO) to derive electronegativity values
• Surface Analysis: Determine solvent-accessible surface area for optimized complex structures
• Polarity Assessment: Compute dipole moments and polarizability tensors
• Partition Coefficient Estimation: Calculate theoretical log P values using fragmentation methods

Software Tools: Gaussian 16, ORCA, or similar computational chemistry packages

LSER Model Application Workflow

The following diagram illustrates the integrated computational and experimental workflow for predicting and validating CB[7]-mediated solubility enhancement:

Experimental Validation Protocol

Phase Solubility Studies

Objective: To experimentally determine solubility enhancement of drugs by CB[7] and validate computational predictions.

Materials:

• CB[7] stock solution (0-30 mM in purified water)
• Drug compounds (high purity, characterized by HPLC)
• Aqueous buffer (appropriate for drug stability)
• Ultrasonic bath
• Thermostated shaking incubator
• UV-Vis spectrophotometer with temperature control
• HPLC system with suitable detection
• Analytical filters (0.45 μm pore size)

Procedure:

• Prepare a series of CB[7] solutions (0, 1, 3, 5, 7, 10, 15 mM) in aqueous buffer
• Add excess drug (approximately 2× predicted solubility) to each CB[7] solution
• Sonicate samples for 1 hour to ensure proper dispersion
• Equilibrate samples with continuous shaking (24 hours, 25°C, protected from light)
• Filter samples through 0.45 μm membrane filters to remove undissolved drug
• Dilute filtrates appropriately with water or mobile phase
• Quantify drug concentration using validated UV-Vis or HPLC methods
• Construct phase solubility diagram by plotting drug solubility against CB[7] concentration

Data Analysis and Binding Constant Determination

For each drug, analyze the phase solubility diagram to determine:

• Solubility enhancement factor (S/Sâ‚€, where Sâ‚€ is intrinsic solubility)
• Binding constant (Kₐ) from the slope of the linear region
• Complexation efficiency (CE = slope/intercept)
• Gibbs free energy of complexation (ΔG = -RTlnKₐ)

Compare experimental results with LSER model predictions to validate computational accuracy.

Research Reagent Solutions

Table 1: Essential Materials for CB[7] Solubility Enhancement Studies

Reagent/Material	Specifications	Function/Application
Cucurbit[7]uril	High purity (>95%), characterized by NMR, MS	Primary host molecule for drug complexation
Drug compounds	Pharmaceutical grade, purity >99% (HPLC)	Guest molecules for solubility enhancement
Aqueous buffers	pH range 3-8, appropriate ionic strength	Maintain physiological conditions
Deuterated solvents	D₂O, DMSO-d₆	NMR characterization of complexes
HPLC mobile phases	MS-grade solvents with modifiers	Analytical quantification of drugs
UV-Vis cuvettes	Quartz, various path lengths	Spectrophotometric measurements

Results and Data Interpretation

Case Study: Experimental vs. Predicted Solubility

Table 2: Experimental and LSER-Predicted Solubility Enhancement for Selected Drugs with CB[7]

Drug	Experimental log S (μM)	LSER-Predicted log S (μM)	Residual	Solubility Enhancement Factor
Cinnarizine	4.137	4.089	+0.048	137.0×
Albendazole	3.851	3.912	-0.061	71.0×
Gefitinib	3.589	3.542	+0.047	38.9×
Triamterene	3.561	3.603	-0.042	36.4×
Vitamin B2	2.972	2.915	+0.057	9.4×
Camptothecin	2.602	2.641	-0.039	4.0×
Zaltoprofen	2.405	2.447	-0.042	2.5×
Cholesterol	1.653	1.698	-0.045	0.5×

The data demonstrates strong correlation between experimental measurements and LSER model predictions, with most residuals falling within ±0.06 log units [24]. The model successfully captures the significant solubility enhancement (up to 137-fold for cinnarizine) achievable through CB[7] complexation.

Structural Insights and Complex Characterization

X-ray crystallography of CB[7]-drug complexes reveals key structural features enabling high-affinity binding:

• Portal interactions: Ion-dipole and hydrogen bonding at carbonyl portals
• Cavity complementarity: Optimal fit of hydrophobic drug moieties within CB[7] cavity
• Minimal host distortion: CB[7] maintains structural integrity with only minor equatorial deformations upon complexation [27]

Thermodynamic profiling indicates that the dissociation constants (Kd) for high-affinity complexes can reach femtomolar ranges, underscoring the exceptional stability of these host-guest systems [25].

Advanced Applications and Formulation Strategies

CB[7] Derivatives for Enhanced Performance

Recent synthetic efforts have focused on CB[7] derivatives to address limitations of the native host:

• Sulfonated CB[7]: Incorporates sulfonate groups on the convex surface to enhance aqueous solubility [27]
• Methylated CB[7]: Displays extraordinary intrinsic solubility (264 mM) though complex solubility may be compromised [27]
• Acyclic analogs: Offer flexible structures with maintained binding affinity and significantly improved solubility profiles [27]

Integration with Complementary Formulation Technologies

CB[7] can be combined with other formulation approaches for synergistic effects:

• Polymer composites: Incorporation into hydrogels or polymeric matrices for controlled release
• Lipid-based systems: Combination with self-emulsifying drug delivery systems
• Supramolecular assemblies: Construction of higher-order structures for targeted delivery

The integration of LSER modeling with CB[7]-mediated solubilization represents a powerful paradigm shift in pharmaceutical development. This case study demonstrates that computational predictions can reliably identify drug candidates amenable to solubility enhancement through CB[7] complexation, potentially reducing experimental screening efforts by up to 70%.

Future directions in this field include:

• Machine learning integration with LSER descriptors for improved predictive accuracy [28] [29]
• High-throughput experimental validation using automated platforms
• Expanded application to biologics, including peptides and protein surfaces
• In vivo correlation studies to translate solubility enhancements to bioavailability improvements

As pharmaceutical pipelines continue to feature increasingly challenging molecules with poor aqueous solubility, the combination of predictive modeling and versatile hosts like CB[7] will play a crucial role in delivering these promising therapeutics to patients.

The Linear Solvation Energy Relationship (LSER) model, also known as the Abraham solvation parameter model, provides a powerful quantitative framework for understanding and predicting solute retention in chromatographic systems [30] [31]. Within the broader context of solubility parameter determination research, LSER enables researchers to characterize chromatographic selectivity according to fundamental solute-solvent interactions, including polarizability, dipolarity, hydrogen bonding, and cavity formation [30]. The general LSER model for chromatography is mathematically expressed as follows [31]:

[ \log k = c + eE + sS + aA + bB + vV ]

In this equation, the uppercase letters (E, S, A, B, V) represent solute-specific descriptors that quantify molecular properties: E (excess molar refraction) indicates solute refractivity, S (dipolarity/polarizability) measures the tendency for dipole-dipole and dipole-induced dipole interactions, A and B quantify hydrogen bond acidity and basicity respectively, and V (McGowan's molecular volume) represents the solute molecular volume [31]. The lowercase letters (c, e, s, a, b, v) are system parameters specific to the chromatographic conditions (stationary and mobile phases) that are independent of the solute [31].

Fast LSER-Based Characterization Protocol for Chromatographic Systems

Principle and Scope

Traditional LSER methods require measuring retention factors for numerous compounds followed by multilinear regression analysis, making them time-consuming and low-throughput [30]. This protocol describes a streamlined approach that carefully selects specific pairs of test compounds which share all molecular descriptors except for one particular property [30]. The selectivity factor of each pair directly reveals the contribution of that specific molecular interaction to chromatographic retention, significantly reducing the number of required experiments while maintaining the informative power of the full LSER model [30]. This method is applicable to both reversed-phase liquid chromatography (RPLC) and hydrophilic interaction liquid chromatography (HILIC) [30].

Materials and Equipment

Table 1: Essential Research Reagent Solutions and Materials

Item Name	Function/Description	Application Notes
Test Solute Pairs	Compounds with similar E, S, A, B, V except one differing descriptor [30]	Enables isolation of specific molecular interactions
Alkyl Ketone Homologues	(C4, C5, C6, C7) for hold-up volume and cavity term determination [30]	Typically four homologues required
HPLC/UHPLC System	Liquid chromatography system with pumping, autosampler, column compartment, and detector	UHPLC provides higher throughput [32]
Chromatography Data System (CDS)	Software for instrument control, data acquisition, and processing [33]	Must provide peak integration and retention time calculation

Experimental Procedure

Step 1: System Preparation and Equilibration

• Install the chromatographic column to be characterized (reversed-phase or HILIC)
• Prepare mobile phase according to required composition (e.g., specific water-organic modifier ratio for RPLC)
• Equilibrate the system with mobile phase until stable baseline is achieved at the specified flow rate

Step 2: Determination of Hold-up Volume and Cavity Term

• Prepare standard solutions of four alkyl ketone homologues (e.g., C4, C5, C6, C7) at appropriate concentrations
• Inject each ketone separately or as a mixture (depending on resolution)
• Record retention times for all ketones
• Plot log k vs. McGowan's molecular volume (V) for the ketone homologues
• Determine the column hold-up volume (tâ‚€) from the intercept and the cavity term (v) from the slope of the regression line [30]

Step 3: Analysis of Selectivity Factor Pairs

• Select and analyze four carefully chosen pairs of test compounds where each pair differs predominantly in one specific molecular descriptor:
  • Pair 1: Different hydrogen bonding acidity (A) but similar E, S, B, V
  • Pair 2: Different hydrogen bonding basicity (B) but similar E, S, A, V
  • Pair 3: Different dipolarity/polarizability (S) but similar E, A, B, V
  • Pair 4: Different polarizability (E) but similar S, A, B, V
• For each pair, calculate the selectivity factor (α) as the ratio of their retention factors (kâ‚‚/k₁)

Step 4: Data Interpretation and System Characterization

• The selectivity factor for each pair directly indicates the system's responsiveness to that specific molecular interaction
• Higher selectivity factors indicate greater system sensitivity to that particular molecular property
• Compare selectivity factors across different chromatographic systems to understand their relative selectivity profiles

Workflow Visualization

Computational Protocol: In Silico Retention Prediction

Principle

This protocol leverages a data-driven methodology to predict retention factors without laboratory experiments by combining quantitative structure-property relationships (QSPR) with LSER and linear solvent strength (LSS) theory [31]. Molecular descriptors are obtained from SMILES string representations of molecules, which are then used to predict solute-dependent parameters for LSER and LSS models [31].

Computational Procedure

Step 1: Molecular Descriptor Generation

• Input molecular structures as SMILES strings
• Calculate molecular descriptors (E, S, A, B, V) using appropriate software or algorithms
• Validate descriptor accuracy against known reference compounds

Step 2: LSER Parameter Determination

• Apply the Abraham solvation parameter model: log k = c + eE + sS + aA + bB + vV
• Use pre-determined system parameters (e, s, a, b, v) for specific chromatographic conditions
• Calculate predicted retention factors for target compounds

Step 3: Mobile Phase Composition Modeling

• Apply linear solvent strength (LSS) theory to account for mobile phase effects: log k = log k₍wâ‚Ž - Sφ
• Where k₍wâ‚Ž is the extrapolated solute retention factor in water, S is the solvent strength parameter, and φ is the volume fraction of organic modifier [31]

Step 4: Retention Time Prediction

• Convert predicted retention factors to retention times using: táµ£ = tâ‚€(1 + k)
• Where tâ‚€ is the system dead time determined experimentally or estimated

Computational Workflow

Data Analysis and Interpretation

LSER System Parameter Table

Table 2: LSER System Parameters and Their Chromatographic Significance

Parameter	Molecular Interaction	Chromatographic Significance	Typical Range
e (Excess molar refraction)	Polarizability via π- and n-electron interactions	Measures stationary phase ability to interact with polarizable solutes	-0.5 to 1.5
s (Dipolarity/Polarizability)	Dipole-dipole and dipole-induced dipole interactions	Indicates system polarity and ability to separate polar compounds	-1.0 to 3.0
a (Hydrogen Bond Acidity)	Solute hydrogen bond basicity with stationary phase hydrogen bond acidity	Important for proton-donor phases; measures hydrogen bond accepting capacity	0.0 to 4.0
b (Hydrogen Bond Basicity)	Solute hydrogen bond acidity with stationary phase hydrogen bond basicity	Critical for proton-acceptor phases; measures hydrogen bond donating capacity	0.0 to 4.0
v (McGowan's Volume)	Cavity formation and dispersion interactions	Related to hydrophobic interactions in RPLC; measures steric selectivity	-0.5 to 2.0

Application Data Table

Table 3: Comparison of Chromatographic Method Development Approaches

Method Characteristic	Traditional Experimental	Fast LSER Characterization	Computational Prediction
Time Requirement	Weeks to months	5 chromatographic runs [30]	Minutes to hours [31]
Compound Requirement	30-50 compounds	4 selective pairs + 4 homologues [30]	Molecular structures only [31]
Primary Application	Fundamental research and method development	Rapid column characterization and screening	High-throughput screening and initial method scouting
Information Obtained	Complete system characterization	Key selectivity differences	Retention time predictions
Experimental Load	High	Moderate	None
Regulatory Acceptance	Well-established	Growing adoption	Emerging acceptance

Application Notes and Technical Considerations

The fast LSER characterization method provides particular value in pharmaceutical analysis where rapid column screening and selection is essential for method development [30] [31]. When implementing this protocol, note that the careful selection of test solute pairs is critical—compounds must be chosen to ensure that only one primary molecular descriptor differs significantly between pair members [30].

For the computational protocol, accuracy depends heavily on the quality of the molecular descriptor calculations and the applicability of the pre-determined system parameters to your specific chromatographic conditions [31]. This approach is particularly valuable in early drug development stages where sample quantities are limited [31].

Both methods align with the growing trend toward digitalization and in-silico modeling in chromatographic science, supporting the implementation of Quality by Design (QbD) principles in analytical method development [31]. The integration of these approaches with modern chromatography data systems (CDS) enables more efficient data management and analysis in regulated laboratory environments [33].

Predicting Partition Coefficients in Polymer-Water Systems for Drug Delivery

Within pharmaceutical development, predicting the distribution of a compound between a polymeric material and an aqueous medium is critical for assessing drug release profiles, stability, and potential patient exposure to leachables. The equilibrium partition coefficient is a key parameter dictating the maximum accumulation of a substance when leaching equilibrium is reached within a product's lifecycle [34]. Linear Solvation Energy Relationships (LSERs) offer a robust, high-performance predictive model for these partition coefficients, moving beyond coarse estimations to accurate, mechanistically-informed predictions [35]. This Application Note details the use of LSERs for determining partition coefficients in low density polyethylene (LDPE)-water systems, framed within broader research on LSER models for solubility parameter determination.

Theoretical Foundation: The LSER Model

The LSER model, or Abraham solvation parameter model, correlates free-energy-related properties of a solute with its molecular descriptors [9]. For partitioning between two condensed phases, the general LSER equation takes the form [9]:

log(P) = cp + epE + spS + apA + bpB + vpVx

Where:

• P is the partition coefficient.
• The lower-case coefficients (cp, ep, sp, ap, bp, vp) are system-specific constants reflecting the solvent's (or phase's) properties.
• The capital letters are solute-specific molecular descriptors.

For the specific case of partitioning between LDPE and water, the following calibrated model has been established [34] [35]:

logKi,LDPE/W = -0.529 + 1.098E - 1.557S - 2.991A - 4.617B + 3.886V

This model has demonstrated high accuracy and precision (n = 156, R² = 0.991, RMSE = 0.264) across a chemically diverse set of compounds [34].

Molecular Descriptor Definitions

The solute descriptors represent specific molecular interaction capabilities and properties [9]:

Table 1: LSER Solute Molecular Descriptors

Descriptor	Name	Molecular Property Represented
E	Excess molar refraction	Characterizes dispersion interactions from n- or π-electrons, corrected for volume
S	Dipolarity/Polarizability	represents the solute's ability to engage in dipole-dipole and dipole-induced dipole interactions
A	Hydrogen Bond Acidity	The solute's ability to donate a hydrogen bond (Lewis acidity)
B	Hydrogen Bond Basicity	The solute's ability to accept a hydrogen bond (Lewis basicity)
V	McGowan's characteristic volume	A measure of the solute's size, related to the endoergic cavity formation energy

Quantitative Data and Model Performance

The LSER model for LDPE-water partitioning was developed using experimental data for 159 compounds spanning a wide range of molecular weight (32 to 722), hydrophobicity (logKi,O/W: -0.72 to 8.61), and polarity [35]. The model's performance was rigorously validated against an independent set of 52 compounds [34].

Table 2: LSER Model for LDPE-Water Partitioning: Performance Benchmarking

Model Scenario	Number of Compounds (n)	Coefficient of Determination (R²)	Root Mean Square Error (RMSE)
Full Model Calibration	156	0.991	0.264
Independent Validation (Experimental Descriptors)	52	0.985	0.352
Independent Validation (Predicted Descriptors)	52	0.984	0.511

The data in Table 2 demonstrates the model's robustness, even when solute descriptors are predicted from chemical structure rather than experimentally determined, a common scenario for new chemical entities [34].

Experimental Protocols

Protocol 1: Direct Experimental Determination of LDPE-Water Partition Coefficients

This protocol outlines the procedure for generating experimental partition coefficient data for model calibration or verification [35].

1. Materials and Reagents

• Low Density Polyethylene (LDPE): Purify via solvent extraction (e.g., with iso-octane and ethanol) to remove additives and impurities [35].
• Aqueous Buffer: Prepare an appropriate buffer relevant to the drug delivery system (e.g., phosphate-buffered saline, pH 7.4).
• Test Compound(s): High-purity certified standards.
• Analytical Instruments: HPLC-MS/GC-MS for quantification, orbital shaker incubator, centrifuge.

2. Experimental Procedure

• Step 1: Preparation. Cut LDPE material into standardized small pieces (e.g., discs or strips) to ensure a high and consistent surface-area-to-volume ratio. Weigh accurately.
• Step 2: Equilibration. Place LDPE pieces in vials containing the aqueous buffer spiked with a known concentration of the test compound. Seal vials to prevent evaporation. Equilibrate in an orbital shaker at a constant temperature (e.g., 25°C or 37°C) until equilibrium is reached (determined by kinetic studies).
• Step 3: Separation. After equilibration, centrifuge the vials if necessary. Carefully separate the LDPE material from the aqueous phase.
• Step 4: Quantification. Analyze the compound concentration in the aqueous phase ([A]aq) before and after equilibration using HPLC-MS/GC-MS. The concentration in the LDPE phase ([A]LDPE) is calculated by mass balance.

3. Data Analysis The partition coefficient is calculated as: Ki,LDPE/W = [A]LDPE / [A]aq Values are typically log-transformed for analysis and modeling: logKi,LDPE/W

Protocol 2: Predicting Partition Coefficients Using the LSER Model

This protocol describes the application of the pre-calibrated LSER model to predict the LDPE-water partition coefficient for a novel compound.

1. Prerequisite Data

• The chemical structure of the target compound.

2. Procedure

• Step 1: Determine Solute Descriptors. Obtain the five LSER molecular descriptors (E, S, A, B, V) for the target compound.
  • Preferred Method: Consult a curated database of experimental solute descriptors (e.g., the UFZ-LSER database).
  • Alternative Method: If experimental descriptors are unavailable, use a Quantitative Structure-Property Relationship (QSPR) prediction tool to compute the descriptors based solely on the compound's chemical structure [34].
• Step 2: Apply the LSER Model. Substitute the obtained descriptors into the calibrated LDPE-water LSER equation: logKi,LDPE/W = -0.529 + (1.098 × E) - (1.557 × S) - (2.991 × A) - (4.617 × B) + (3.886 × V)
• Step 3: Interpret Result. The output is the predicted logKi,LDPE/W. A higher value indicates a greater tendency of the compound to partition into the LDPE polymer rather than remain in the aqueous phase.

Figure 1: Workflow for predicting LDPE-water partition coefficients using the LSER model.

The Scientist's Toolkit: Key Reagents and Materials

Table 3: Essential Research Reagent Solutions and Materials

Item	Function/Application	Critical Notes
Purified LDPE	The polymeric phase for partitioning studies.	Purification via solvent extraction is critical to remove additives that interfere with sorption measurements [35].
n-Octanol	Reference solvent for measuring lipophilicity (logKow).	logKow provides a useful baseline and can be used in log-linear models for non-polar compounds [36] [35].
Abraham Solute Descriptors	The core input parameters for the LSER model.	Can be sourced from experimental databases or predicted via QSPR methods [34] [9].
Aqueous Buffers (e.g., PBS)	Simulates the physiological aqueous medium.	Buffer composition and pH must be controlled and reported, as pH affects the ionization state of ionizable compounds [36].
Chemical Standards	For calibration and method validation.	A chemically diverse training set is crucial for developing a robust and generalizable LSER model [34].
5-Lox-IN-5	`5-Lox-IN-5|Potent 5-LOX Inhibitor for Research`	5-Lox-IN-5 is a potent 5-lipoxygenase (5-LOX) inhibitor for research use only (RUO). It blocks leukotriene biosynthesis to study inflammation, cancer, and related pathways.

Discussion and Comparison with Other Polymers

The sorption behavior of LDPE can be compared to other common polymers like polydimethylsiloxane (PDMS), polyacrylate (PA), and polyoxymethylene (POM) by comparing their respective LSER system parameters [34]. LDPE, a non-polar polyolefin, primarily interacts via dispersion forces. In contrast, polymers like PA and POM, which contain heteroatoms, offer capabilities for stronger polar and hydrogen-bonding interactions.

For polar, non-hydrophobic compounds (with logKi,LDPE/W values up to 3-4), POM and PA exhibit stronger sorption than LDPE. For highly hydrophobic compounds (logKi,LDPE/W > 4), all four polymers exhibit roughly similar sorption behavior [34]. This comparative analysis is invaluable for selecting the appropriate polymer for a specific drug delivery application.

Figure 2: Logical relationships between sorbate properties and polymer selection based on interaction capabilities. LDPE strongly sorbs non-polar compounds, while polar polymers like PA and POM have a higher affinity for polar sorbates [34].

Integrating DFT Calculations for LSER Parameter Determination

Linear Solvation Energy Relationships (LSERs) represent a powerful quantitative approach for predicting solute partitioning and solvation behavior across diverse chemical systems. The integration of Density Functional Theory (DFT) calculations has revolutionized LSER parameter determination, moving beyond traditional experimental derivation methods to computationally-driven approaches. This protocol details the integration of DFT calculations, particularly the widely-used B3LYP functional, for accurate prediction of LSER solute descriptors, enabling robust solvation property prediction within pharmaceutical and environmental research contexts.

Linear Solvation Energy Relationships provide a multi-parameter equation system that correlates solute transfer free energies between phases with fundamental molecular interactions. The standard LSER model takes the form:

log SP = c + eE + sS + aA + bB + vV

Where SP represents the solvation property of interest (e.g., partition coefficient, solubility), and the capital letters represent solute-specific descriptors: E (excess molar refractivity), S (dipolarity/polarizability), A (hydrogen-bond acidity), B (hydrogen-bond basicity), and V (McGowan characteristic molecular volume) [37]. The lower-case letters are system-specific coefficients that are determined empirically for each particular chemical system or process.

Traditional LSER parameter determination relied heavily on experimental measurements of partition coefficients in well-characterized systems. However, the emergence of DFT calculations has enabled first-principles computation of these descriptors, significantly expanding the applicability of LSER models to compounds lacking extensive experimental data [38] [39]. This computational approach aligns with the growing need for predictive toxicology and drug development tools that can accurately forecast solubility and partitioning behavior early in the research pipeline.

Computational Framework

DFT Method Selection

The selection of appropriate DFT functionals and basis sets represents a critical foundation for accurate LSER parameter prediction:

Table 1: Recommended DFT Methods for LSER Parameter Calculations

Computational Component	Recommended Method	Key Applications	References
Primary Functional	B3LYP (Becke, 3-parameter, Lee-Yang-Parr)	General geometry optimization, electronic property calculation	[40] [41]
Alternative Functional	B3PW91	Systems requiring improved treatment of correlation effects	[40]
Basis Set	6-311G*	Standard prediction of molecular volumes and electrostatic properties	[42]
Extended Basis Set	6-311++G(d,p)	Systems with diffuse electron clouds or requiring higher accuracy	[41]

The B3LYP functional has demonstrated particular effectiveness for LSER applications due to its hybrid nature, incorporating a mixture of Hartree-Fock exchange with DFT exchange-correlation. The functional is expressed as:

E^B3LYPXC = (1 - a)E^LSDAX + aE^HFX + bE^B88X + cE^LYPC + (1 - c)E^VWNC

where a = 0.20, b = 0.72, and c = 0.81, with these coefficients having been empirically optimized for accurate prediction of molecular properties [40]. For the 6-311G* basis set, frequency calculations should incorporate a scaling factor of 0.966 to correct for systematic vibrational frequency overestimation [42].

Solvation Models

Continuum solvation models are essential for accurate LSER parameter determination as they account for bulk solvent effects:

• Polarizable Continuum Model (PCM): Represents the solvent as a dielectric continuum with a cavity representing the solute. This model effectively captures long-range electrostatic interactions but has limitations for specific solute-solvent interactions like hydrogen bonding [42].

• SMD Model (Solvation Model based on Density): A modern continuum model that computes solvation free energies (ΔG) comprising long-range electrostatic (ΔGelec) and short-range non-electrostatic components (ΔGnon-elec). The SMD model provides improved accuracy for partition coefficient prediction, particularly for systems involving significant cavitation energy requirements [42].

Protocol: DFT-Assisted LSER Parameter Determination

The following diagram illustrates the integrated computational-experimental workflow for DFT-assisted LSER parameter determination:

Step-by-Step Computational Procedure

Step 1: Molecular Structure Preparation and Optimization

• Initial Structure Generation: Construct molecular structures using chemical drawing software (e.g., ChemDraw, Avogadro) or retrieve from databases (PubChem, ChemSpider).

• Geometry Optimization: Perform full geometry optimization using B3LYP/6-311G* method without symmetry constraints:

  Optimization convergence criteria should include force thresholds <0.00045 Hartree/Bohr and displacement thresholds <0.0018 Bohr.

• Frequency Verification: Confirm optimization to true minima by absence of imaginary frequencies in vibrational analysis.

Step 2: Electronic Property Calculations

• Electrostatic Potential Mapping: Calculate molecular electrostatic potential using the optimized structure at the same theory level.

• Orbital Analysis: Determine frontier molecular orbitals (HOMO/LUMO) and their energies for reactivity assessment.

• Atomic Partial Charges: Compute natural bond orbital (NBO) charges or Mulliken population analysis.

Step 3: Specific Descriptor Calculations

• Molecular Volume (V): Calculate from the molecular mass and computed three-dimensional structure using the McGowan approach:

  • V = (Molecular Weight/Density) - 6.56 × Number of non-hydrogen atoms
  • Alternatively, compute using Monte Carlo integration of the molecular cavity volume.

• Hydrogen-Bond Acidity (A) and Basicity (B):

  • Determine A from calculated hydrogen bond dissociation energies or molecular electrostatic potential minima near acidic hydrogens.
  • Calculate B from proton affinity values or electrostatic potential maxima near basic atoms.

• Dipolarity/Polarizability (S):

  • Compute from molecular dipole moment and polarizability tensor calculations.
  • Alternative approach: Derive from solvatochromic shift calculations in different solvents.

• Excess Molar Refractivity (E):

  • Calculate from the computed molecular polarizability and refractive index relationships.

Experimental Validation Protocol

While DFT calculations provide initial LSER parameter estimates, experimental validation remains essential:

• Chromatographic Measurements:

  • Perform reverse-phase HPLC with standardized stationary phases (C18, cyano-propyl).
  • Measure retention factors for at least 15 reference compounds with known LSER parameters.
  • Use methanol/water or acetonitrile/water mobile phases with varying compositions.

• Partition Coefficient Determination:

  • Measure solute partitioning in octanol-water systems using shake-flask or generator column methods.
  • For polymer-water systems (e.g., LDPE-water), use controlled stirring and equilibrium establishment over 24-48 hours [37].
  • Analyze solute concentrations using HPLC-UV or GC-MS.

• Data Correlation:

  • Correlate experimental partition coefficients with calculated LSER parameters using multiple linear regression.
  • Apply statistical validation (leave-one-out cross-validation, external test sets).

Application Notes

Case Study: Pharmaceutical Compound Partitioning

Recent research demonstrates the successful application of DFT-assisted LSER for predicting low density polyethylene-water partition coefficients (log K_{i,LDPE/W}) for pharmaceutical compounds. The developed LSER model:

log K_{i,LDPE/W} = -0.529 + 1.098E - 1.557S - 2.991A - 4.617B + 3.886V

showed exceptional predictive accuracy (n = 156, R² = 0.991, RMSE = 0.264) when using DFT-calculated descriptors [37]. This approach enables reliable prediction of contaminant migration from plastic packaging into pharmaceutical formulations.

Case Study: Aromatic Contaminant Adsorption

DFT-assisted LSER modeling has successfully predicted multi-walled carbon nanotube (MWCNT) adsorption of aromatic contaminants. The molecular volume descriptor (V) dominated adsorption at all concentrations, while hydrogen-bond accepting (B) and donating (A) capabilities became significant at higher equilibrium concentrations [39]. This insight guides nanomaterial selection for water treatment applications.

Troubleshooting Guide

Table 2: Common Computational Challenges and Solutions

Challenge	Potential Cause	Solution
Poor LSER correlation	Inaccurate volume calculations	Implement explicit volume integration instead of group contribution methods
Overestimation of H-bond capabilities	Insufficient electron correlation	Apply dispersion-corrected functionals (e.g., ωB97X-D) or double-hybrid functionals
Systematic deviation for specific compound classes	Missing specific interactions	Incorporate explicit solvent molecules for strong H-bonding systems
Unphysical vibrational frequencies	Basis set superposition error	Apply counterpoise correction or use larger basis sets

Research Reagent Solutions

Table 3: Essential Computational Tools for DFT-LSER Integration

Tool Category	Specific Examples	Key Function	Application Notes
Quantum Chemistry Software	Gaussian 09, Gaussian 16	DFT calculations, geometry optimization, frequency analysis	SMD model implementation available [42]
Visualization & Analysis	GaussView, ChemCraft	Molecular structure building, vibrational frequency animation, results analysis	Critical for verifying optimized geometries and vibrational assignments [42]
Descriptor Calculation	DRAGON, COSMOmic	LSER parameter computation from molecular structure	Alternative to manual descriptor calculation
Statistical Analysis	R, Python (scikit-learn), MATLAB	Multiple linear regression, model validation, statistical analysis	Essential for LSER model development and cross-validation
Solvation Databases	FreeSolv, CompTox	Experimental solvation free energies, partition coefficients	Critical for model validation and benchmarking [37]

The integration of DFT calculations with LSER modeling represents a powerful paradigm shift in solvation property prediction. The B3LYP/6-311G* method, combined with continuum solvation models like PCM or SMD, provides accurate computation of fundamental LSER descriptors directly from molecular structure. This approach enables researchers to develop predictive models for diverse applications including pharmaceutical solubility prediction, environmental contaminant transport, and adsorption process optimization. The continued refinement of DFT methodologies promises further enhancement of LSER predictive capabilities across chemical space.

Overcoming LSER Limitations: Strategies for Robust and Predictive Models

Common Pitfalls in LSER Model Development and How to Avoid Them

Linear Solvation Energy Relationships (LSERs), also known as the Abraham model, are a powerful tool for predicting solute transfer processes across various chemical and biological systems. Within pharmaceutical research, they are invaluable for estimating key properties such as solubility, permeability, and partition coefficients, which are critical in drug development. The model's foundation lies in correlating a free-energy related property of a solute with its molecular descriptors, capturing the balance of different intermolecular interactions. However, the development of a robust, predictive LSER model is fraught with potential missteps that can compromise its accuracy and applicability. This application note outlines the common pitfalls encountered during LSER model development and provides detailed protocols to avoid them, ensuring the creation of reliable models for solubility parameter determination and related research.

Common Pitfalls and Strategic Avoidance

The journey from conceptualizing an LSER model to its successful application requires careful attention to detail. The following table summarizes the most frequent challenges and their solutions.

Table 1: Common Pitfalls in LSER Model Development and How to Mitigate Them

Pitfall Category	Description of the Pitfall	Consequences	Strategies for Avoidance
Data Quality & Diversity	Using a small, chemically homogeneous, or unreliable dataset for model training.	Poor model predictability and limited application domain; the model fails for new chemical classes. [34] [9]	- Use a large number of compounds (>50 is a starting point).- Ensure chemical diversity covers the intended application space.- Use experimental descriptor values from curated databases where possible. [34] [43]
Descriptor Selection & Handling	Incorrectly using solute descriptors (E, S, A, B, V, L) or misinterpreting their physical meaning.	Model coefficients (e, s, a, b, v) lose their physical interpretability, leading to incorrect conclusions about molecular interactions. [9] [43]	- Never use a descriptor set without confirming its applicability to your specific system (e.g., Eq. 1 vs. Eq. 2 for different phase transfers). [9]- Validate descriptors for a subset of compounds if possible.
Model Validation & Overfitting	Relying solely on goodness-of-fit (e.g., R²) for a single dataset without rigorous internal and external validation.	An overfitted model that appears excellent for training data but has poor predictive power for new compounds. [34] [44]	- Use internal validation (e.g., cross-validation, leave-one-out).- Use a strict external validation set (~25-33% of total data) not used in model training. [34]- Report multiple metrics (R², RMSE, CCC, etc.). [44]
Theoretical Linearity Assumption	Blindly applying the LSER linear model to systems involving strong, specific interactions without verifying the linearity premise.	The model may not adequately capture the thermodynamics of the system, such as strong hydrogen bonding, leading to systematic errors. [9]	- Understand the thermodynamic basis of LSER linearity. [9]- Examine residuals for non-random patterns that suggest non-linearity.
Interpretation of System Coefficients	Incorrectly assigning physical meaning to the fitted system coefficients (e, s, a, b, v) without considering the specific model form.	Misunderstanding the dominant interactions in the system (e.g., misidentifying the key driver for retention or partitioning). [9] [43]	- Recall that coefficients are complementary properties of the solvent/phase system. [9] [43]- Compare coefficients with those from well-characterized systems for context.

Experimental Protocol for Robust LSER Model Development

This protocol provides a step-by-step guide for developing a statistically sound LSER model, incorporating checks to avoid the common pitfalls outlined above.

Phase I: Data Collection and Curation

Objective: To assemble a high-quality, representative dataset for model training and validation.

• Define the System and Property: Clearly define the system under study (e.g., partition coefficient between low-density polyethylene and water, log KLDPE/W) and the free-energy related property (log P) to be modeled. [34]
• Solute Selection: Select a minimum of 50-60 solutes, aiming for more if possible. [43] The solutes must:
  • Be Chemically Diverse: Cover a wide range of values for each molecular descriptor (E, S, A, B, V). [34]
  • Be Relevant: Include compounds structurally related to the final application domain (e.g., drug-like molecules for pharmaceutical studies). [24]
• Data Sourcing:
  • Experimental Data: Source experimental values for the property of interest (log P) from reliable, peer-reviewed literature. Document experimental conditions (temperature, pH, etc.).
  • Solute Descriptors: Prioritize obtaining experimentally derived LSER solute descriptors from curated databases like the UFZ-LSER database. If experimental descriptors are unavailable for all compounds, predicted descriptors from Quantitative Structure-Property Relationship (QSPR) tools can be used, but this may increase prediction error (e.g., RMSE can increase, as shown in one study from 0.352 to 0.511). [34]
• Data Splitting: Randomly divide the full dataset into a training set (approximately 67-75%) for model development and a validation set (approximately 25-33%) for final model testing. The validation set must be locked away and not used during the model fitting process. [34]

Phase II: Model Fitting and Internal Validation

Objective: To construct the LSER model and assess its internal stability.

• Model Equation Selection: Choose the correct LSER equation for your system.
  • For partitioning between two condensed phases (e.g., water/solvent): log SP = c + eE + sS + aA + bB + vV [9] [43]
  • For gas-to-solvent partitioning: log SP = c + eE + sS + aA + bB + lL [9]
• Multiple Linear Regression (MLR): Perform MLR analysis using the training set to determine the system coefficients (c, e, s, a, b, v/l).
• Internal Validation:
  • Goodness-of-fit: Calculate R² and Root Mean Square Error (RMSE) for the training set.
  • Cross-Validation: Perform k-fold cross-validation (e.g., 10-fold) or leave-one-out cross-validation on the training set. Calculate the cross-validated R² (Q²) and RMSE from cross-validation (RMSECV). A high Q² and a small difference between R² and Q² indicate a robust model that is not overfitted. [44]

Phase III: Model Validation and Interpretation

Objective: To rigorously test the model's predictive power and interpret the results.

• External Validation: Use the locked validation set from Phase I. Predict the property for these compounds using the model developed in Phase II.
  • Calculate the coefficient of determination (R²test), RMSE of prediction (RMSEP), and the Concordance Correlation Coefficient (CCC) between predicted and experimental values. [44]
  • A model is considered predictive only if it performs well on this external set.
• Residual Analysis: Plot residuals (predicted vs. experimental values) for both training and validation sets. Look for random scatter; any systematic pattern suggests a flaw in the model or the linearity assumption. [9]
• Coefficient Interpretation: Analyze the sign and magnitude of the fitted system coefficients.
  • A positive 'v' coefficient often indicates the cavity term and dispersion interactions are favorable for retention/sorption in that phase. [43]
  • A negative 'b' coefficient indicates the phase acts as a hydrogen-bond acid, and solute basicity (B) reduces partitioning into that phase. [43]
  • Compare your coefficients with those from similar systems in the literature for context. [43]

The entire workflow, with its critical decision points, is summarized in the following diagram:

Diagram Title: LSER Model Development Workflow

Building a reliable LSER model requires specific computational and data resources. The following table details the essential components of the researcher's toolkit.

Table 2: Essential Reagents and Resources for LSER Modeling

Category	Item / Resource	Function / Description	Key Considerations
Data Sources	UFZ-LSER Database	A curated, freely accessible database of experimental LSER solute descriptors.	The primary source for reliable, experimentally derived molecular descriptors. [9]
	Peer-Reviewed Literature	Source of experimental partition coefficients, solubility data, and retention factors (log P, log S, log k).	Critical for building the property dataset. Must document experimental conditions. [34] [24]
Software & Algorithms	Statistical Software (R, Python)	Platform for performing Multiple Linear Regression (MLR) analysis and calculating validation metrics.	Essential for model fitting and internal validation (e.g., cross-validation). [44] [43]
	QSPR Prediction Tools	Software for predicting LSER solute descriptors when experimental values are unavailable.	Can introduce error; use with caution and validate predictions where possible. [34]
Theoretical Framework	Abraham LSER Equations	The core mathematical models describing solute transfer between phases.	Using the wrong equation (e.g., using V instead of L for gas/solvent systems) is a fatal error. [9]
	Chemometric Principles	Guidelines for model validation (cross-validation, external validation, Roy-metrics).	Non-negotiable for proving model robustness and predictive power. [44]

The development of a predictive LSER model is a meticulous process that extends beyond a simple linear regression. Success hinges on the quality and diversity of the underlying data, the correct application and interpretation of the model's parameters, and, most critically, a rigorous and multi-faceted validation strategy. By recognizing common pitfalls—such as dataset limitations, overfitting, and theoretical missteps—and adhering to the detailed protocols and checks outlined in this document, researchers can build reliable LSER models. These robust models will serve as powerful tools in the determination of solubility parameters and the prediction of key physicochemical properties, ultimately accelerating drug development and materials design.

Addressing Challenges with Strong Hydrogen Bonding and Polar Compounds

The accurate prediction of solubility for compounds with strong hydrogen bonding and polar characteristics remains a significant challenge in pharmaceutical and chemical development. Traditional solubility parameters, such as the foundational Hildebrand parameter (a single value derived from cohesive energy density), often fail to account for the complex, specific interactions of hydrogen-bonding and highly polar molecules [21] [45]. This limitation can lead to inaccurate predictions of miscibility, solubility, and partitioning behavior, impacting drug formulation, polymer design, and solvent selection.

The Linear Solvation Energy Relationship (LSER) model, developed by Abraham, provides a more nuanced framework by deconstructing intermolecular interactions into distinct, quantitatively addressable components [9] [20]. This application note details protocols for leveraging the LSER model and its modern derivatives, specifically Partial Solvation Parameters (PSP), to overcome the challenges posed by strong hydrogen-bonding and polar compounds within a rigorous thermodynamic context [21] [20].

Theoretical Framework: LSER and Partial Solvation Parameters

The LSER Model and Molecular Descriptors

The core LSER model correlates free-energy-related properties of a solute with six fundamental molecular descriptors [9] [46]. These descriptors capture the solute's capacity for different interaction types, allowing for a multiparameter analysis of solubility.

Table 1: Abraham's LSER Molecular Descriptors

Descriptor	Symbol	Physical Interpretation
McGowan's Characteristic Volume	Vx	Characteristic volume; encodes cavity formation and dispersion interactions [9].
Gas-Hexadecane Partition Coefficient	L	Determined from gas-liquid partition coefficient in n-hexadecane at 298 K [9].
Excess Molar Refraction	E	Characterizes polarizability due to π- and n-electrons [9].
Dipolarity/Polarizability	S	Reflects the solute's ability to engage in dipole-dipole and dipole-induced dipole interactions [9].
Hydrogen Bond Acidity	A	Quantifies the solute's ability to donate a hydrogen bond (proton donor strength) [9].
Hydrogen Bond Basicity	B	Quantifies the solute's ability to accept a hydrogen bond (proton acceptor strength) [9].

For solute transfer between condensed phases, the LSER model is expressed as: log(P) = c_p + e_pE + s_pS + a_pA + b_pB + v_pV_x [9] Here, the lower-case coefficients (e.g., a_p, b_p) are system-specific parameters that describe the complementary properties of the solvent or phase system.

The Advent of Partial Solvation Parameters (PSP)

The Partial Solvation Parameter (PSP) approach bridges the LSER framework with equation-of-state thermodynamics, offering a cohesive method for characterizing pure fluids, mixtures, and interfaces [20]. PSPs are defined directly from LSER descriptors, facilitating the transfer of a vast body of existing LSER data into a thermodynamically robust model. The four key PSPs are [20]:

• Dispersion PSP (σ_d): Reflects hydrophobicity, cavity effects, and weak non-polar interactions. It maps the V_x and E LSER descriptors.
• Polarity PSP (σ_p): Reflects combined Keesom (dipole-dipole) and Debye (dipole-induced dipole) interactions. It maps the S LSER descriptor.
• Acidity PSP (σ_Ga) & Basicity PSP (σ_Gb): These are Gibbs free-energy descriptors that specifically reflect the hydrogen-bonding or Lewis acid/base character of the molecule. They map the A and B LSER descriptors, respectively.

A key advantage of the PSP framework is its ability to directly estimate the free energy change (ΔG_HB) upon hydrogen bond formation using the acidity and basicity parameters [20]: -ΔG_{HB, 298} = 2V_mσ_Gaσ_Gb = 20000AB

This quantitative linkage allows for a more profound analysis of the role of hydrogen bonding in solubility and miscibility.

Experimental Protocols

Protocol 1: Determination of LSER Descriptors via Inverse Gas Chromatography (IGC)

Principle: IGC is a powerful technique for characterizing the surface and bulk thermodynamic properties of solids, including active pharmaceutical ingredients (APIs). It involves injecting known probe gases onto a chromatographic column containing the drug sample and measuring their retention times [20].

Materials:

• Analyte: The solid drug compound of interest.
• Probe Gases: A selected series of 6-10 vapors with known and diverse LSER descriptors (e.g., n-alkanes, alcohols, ketones, ethers, chlorinated compounds).
• Instrumentation: Gas chromatograph equipped with a flame ionization detector (FID) and temperature-controlled oven.
• Column Preparation: The solid drug is uniformly packed into a silanized glass column.

Procedure:

• Conditioning: Condition the prepared column in the GC oven under a flow of carrier gas (e.g., Helium or Nitrogen) at a temperature slightly below the compound's melting point for several hours to remove volatile contaminants and establish a stable baseline.
• Probe Injection: Inject a series of probe gases at infinite dilution (small, symmetric peaks) into the column. For each probe, perform injections at at least three different temperatures (e.g., 30°C, 40°C, 50°C) to assess temperature dependence.
• Data Recording: Record the net retention volume (V_N) for each probe gas at each temperature. The V_N is calculated from the retention time and the carrier gas flow rate.
• Activity Coefficient Calculation: Calculate the activity coefficient at infinite dilution (γ^∞) and the related energy of interaction for each probe using standard thermodynamic relationships from the V_N data.
• Multilinear Regression: Perform a multilinear regression analysis where the measured thermodynamic property (e.g., log of the partition coefficient) is the dependent variable, and the known LSER descriptors of the probe gases are the independent variables. The resulting regression coefficients provide the LSER descriptors for the solid drug analyte [20].

Protocol 2: Predicting Drug Solubility in Solvent Systems Using PSPs

Principle: Once the LSER descriptors for a drug are known (from IGC, database, or in silico methods), its PSPs can be calculated. These PSPs are then used within a thermodynamic model to predict solubility in pure solvents or complex mixtures [20].

Materials:

• Data: LSER descriptors (V_x, E, S, A, B) for the drug and the target solvent(s).
• Software: Computational environment capable of performing basic calculations (e.g., Python with NumPy/SciPy, MATLAB, or a dedicated spreadsheet).

Procedure:

• Calculate PSPs: Compute the Partial Solvation Parameters for both the solute (drug) and the solvent using the defined relationships [20]:
  • σ_d = 100 * (3.1V_x + E) / V_m
  • σ_p = 100 * S / V_m
  • σ_Ga = 100 * A / V_m
  • σ_Gb = 100 * B / V_m (Where V_m is the molar volume of the compound.)
• Estimate Hydrogen-Bonding Free Energy: Calculate the free energy change upon hydrogen bond formation between the drug and solvent using the PSPs [20]:
  • ΔG_HB = - (30,450 - 35.1T) * A_drug * B_solvent (and the complementary A_solvent * B_drug)
• Compute Activity Coefficients: Use the PSPs within an equation-of-state model (e.g., those based on the Quasi-Chemical theory) or a suitable activity coefficient model (e.g., UNIQUAC) to calculate the activity coefficient of the drug at infinite dilution (γ^∞) in the solvent.
• Predict Solubility: The mole fraction solubility (x_sat) of the solid drug can be predicted using the following fundamental thermodynamic relation, where the activity coefficient accounts for the non-ideality of the solution:
  • log(x_sat) = - [ΔH_fus / (2.303R)] * (1/T - 1/T_m)] - log(γ^∞) (Where ΔH_fus is the enthalpy of fusion of the drug, T_m is its melting point, and T is the temperature of interest.)

Data Presentation and Analysis

Comparative Parameter Tables

Table 2: Comparison of Solubility Parameter Frameworks for Hydrogen-Bonding Compounds

Framework	Key Parameters	Handling of H-Bonding	Primary Application Scope
Hildebrand	δ (single parameter)	Not accounted for separately.	Non-polar and slightly polar systems [45].
Hansen (HSP)	δd, δp, δhb	Single, combined parameter (δhb); does not differentiate acidity from basicity [21] [45].	Solvent selection for polymers, paints, inks [45].
LSER (Abraham)	Vx, E, S, A, B	Separate, specific descriptors for Acidity (A) and Basicity (B) [9] [20].	Prediction of partition coefficients, solubility, and biomolecular partitioning [20] [46].
PSP	σd, σp, σGa, σGb	Separate, thermodynamically-defined Acidity (σGa) and Basicity (σGb) PSPs; enables ΔGHB calculation [20].	Cohesive thermodynamic framework for bulk phases and interfaces; miscibility prediction [20].

Table 3: Illustrative Solubility Data for Naproxen in Binary Solvent Mixtures (at 298.15 K)

Solvent System	Mass Fraction of Alcohol	Experimental Solubility (mole fraction)	Notes
1-Propanol + Ethylene Glycol	0.50	1.25 x 10-3	Higher solubility attributed to favorable H-bonding and molecular interactions [47].
2-Propanol + Ethylene Glycol	0.50	9.80 x 10-4	Lower solubility despite 2-PrOH's lower polarity, highlighting role of molecular structure [47].
1-Propanol (Neat)	1.00	1.52 x 10-3	---
2-Propanol (Neat)	1.00	1.18 x 10-3	---

The Scientist's Toolkit: Key Reagent Solutions

Table 4: Essential Research Reagents for LSER/PSP Experimental Characterization

Reagent / Material	Function / Application	Example Probes for IGC
n-Alkane Series (e.g., n-hexane, n-heptane, n-octane)	To characterize dispersion interactions and determine the McGowan volume (Vx) contribution [20].	n-Heptane, n-Octane
Chlorinated Alkanes (e.g., dichloromethane, chloroform)	To probe polarizability and weak dipole interactions. Chloroform can also act as a weak H-bond acid.	Dichloromethane
Ethers (e.g., diethyl ether, tetrahydrofuran)	To characterize the solid's H-bond basicity (as acceptors) and polar interactions [20].	Diethyl Ether
Ketones (e.g., acetone, butanone)	To probe dipolarity/polarizability (S) and H-bond basicity.	Acetone
Alcohols (e.g., ethanol, 1-butanol)	To characterize the solid's H-bond acidity (as donors) and basicity (as acceptors) via descriptors A and B [20].	Ethanol, 1-Butanol
Ethylene Glycol	A co-solvent with strong H-bonding character; used in binary mixtures to modulate solvent environment and study cosolvency effects [47].	N/A (as solvent)

The LSER model and its thermodynamic extension via Partial Solvation Parameters provide a powerful, descriptor-based framework for addressing the complex solubility behavior of strong hydrogen-bonding and polar compounds. The critical advancement lies in the explicit separation of hydrogen-bonding acidity and basicity, moving beyond the combined single parameter used in earlier models [21] [20]. This allows for the "complementarity matching" principle of solubility—where a good solvent for a solute may have complementary, rather than just similar, properties (e.g., a strong acid with a strong base)—to be quantitatively integrated into predictions.

The presented protocols for determining molecular descriptors via Inverse Gas Chromatography and applying them through the PSP framework offer researchers a robust methodological pathway. The ability to connect these descriptors to thermodynamic properties like the hydrogen-bonding free energy and activity coefficients enables more reliable predictions of solubility, partition coefficients, and polymer-drug miscibility, which are critical in pharmaceutical development [20] [46]. While machine learning models are emerging as powerful predictive tools, the LSER/PSP approach retains a significant advantage through its physicochemical interpretability, providing not just a prediction but also an explanation rooted in molecular interactions [45].

The Role of Quantum Chemical Calculations (COSMO-RS) in Parameter Prediction

The accurate prediction of solubility, partition coefficients, and other physicochemical parameters is fundamental to drug development and environmental science. For decades, Linear Solvation Energy Relationship (LSER) models have served as valuable predictive tools, correlating molecular descriptors with solvation energies and partition coefficients [14] [34]. However, a significant limitation of traditional LSER approaches has been their reliance on experimental data for parameterization, restricting their application to novel compounds [14] [12]. The integration of quantum chemical calculations, particularly the COnductor-like Screening MOdel for Real Solvents (COSMO-RS), is transforming this field by providing an a priori predictive pathway for obtaining crucial molecular parameters, thereby extending the capabilities of LSER models into a more powerful, computationally-driven framework [14] [48] [12].

COSMO-RS acts as a bridge between quantum mechanics and thermodynamic properties of liquids. It starts with quantum chemical calculations of individual molecules in a virtual conductor environment, then uses statistical thermodynamics to predict the solvation properties of these molecules in real solvents [48]. This methodology provides a physical basis for the parameters used in LSER models, moving beyond pure correlation towards a more fundamental understanding of solute-solvent interactions [12]. The fusion of these approaches is particularly relevant for quantifying hydrogen-bonding contributions to solvation enthalpy and free energy—a critical factor in predicting drug solubility and partitioning behavior [14].

Theoretical Foundation: Integrating COSMO-RS with LSER Frameworks

The LSER Model and Its Limitations

Abraham's LSER model utilizes linear equations to quantify solute transfer between phases. For solute partitioning between gas and liquid phases, the model takes the form: log(K) = c + eE + sS + aA + bB + lL [14] [12]

The uppercase letters (E, S, A, B, L, Vx) represent solute-specific molecular descriptors: excess molar refraction, dipolarity/polarizability, hydrogen-bond acidity, hydrogen-bond basicity, the gas-hexadecane partition coefficient, and McGowan's characteristic volume, respectively [14] [34]. The lowercase letters are complementary system-specific coefficients obtained through multilinear regression of experimental data [14].

While remarkably successful, the traditional LSER approach faces two primary challenges:

• Experimental Dependency: The determination of solute descriptors and system coefficients relies heavily on extensive experimental data, limiting predictive application for novel compounds [12].
• Thermodynamic Inconsistency: The current parameterization can lead to peculiar results for self-solvation of hydrogen-bonded compounds, violating the expected equality of complementary interaction energies when solute and solvent are identical [12].

COSMO-RS as a Quantum Chemical Foundation

COSMO-RS addresses these limitations by deriving solvation properties from first principles. The methodology involves:

• Quantum Chemical Calculation: Each molecule undergoes density functional theory (DFT) calculation in a virtual conductor environment, yielding a detailed surface charge distribution (σ-profile) [49] [12].
• Surface Interaction Statistics: The statistical thermodynamics of surface segment interactions between solute and solvent are computed, based on the respective σ-profiles [14] [48].
• Property Prediction: Chemical potentials, activity coefficients, solvation free energies, and partition coefficients are derived from these interactions [49].

A key advantage of COSMO-RS is its capacity to calculate the hydrogen-bonding contribution to solvation enthalpy—a crucial component often requiring estimation in other models [14]. Furthermore, the σ-profiles and polarity distributions obtained can be translated into LSER-compatible descriptors, creating a seamless quantum-to-thermodynamic pipeline [12].

Computational Protocols and Application Notes

Protocol 1: Prediction of Partition Coefficients Using COSMO-RS

This protocol details the calculation of partition coefficients (e.g., log P) for small drug-like molecules between organic solvents and water using COSMO-RS [49].

Workflow Overview:

Step-by-Step Procedure:

• Input Structure Acquisition: Obtain initial 3D molecular structures from reliable databases such as ChemSpider (www.chemspider.com). Structures should be in standard file formats (e.g., .mol, .sdf) [49].
• Primary Geometry Optimization: Perform initial quantum chemical geometry optimization using the TURBOMOLE package (v.7.1 or higher). Employ density functional theory (DFT) with appropriate functional (e.g., BP86) and basis set (def2-TZVP) [49].
• Conformer Generation and Selection: Use COSMOconf (v.4.1 or higher) for comprehensive conformation generation. Input the optimized structure from Step 2. Generate multiple conformers through arbitrary distortion and select the energetically most favorable ones for subsequent steps [49].
• σ-Profile Calculation: Calculate the σ-profile for the conformer set using triple ζ valence electron plus polarization with diffusion function (TZVPD-FINE) parametrization. This provides the detailed screening charge density distribution for each molecule [49].
• COSMOtherm Database Integration: Import the resulting σ-profiles into the COSMOtherm (v.17.0 or higher) compound database. Utilize existing parametrization for solvents (water, organic solvents) from the built-in database [49].
• Chemical Potential Calculation: Calculate the chemical potential of the solute molecule at infinite dilution in both aqueous and organic phases, considering surface interactions with the surrounding solvent [49].
• Partition Coefficient Determination: Compute the partition coefficient from the difference in chemical potentials between the two phases: log P = -Δμ / (RT ln 10). Account for additional system components such as salt or glycerine concentration if present [49].

Protocol 2: Deriving LSER Descriptors from Quantum Chemistry

This protocol describes the calculation of Abraham LSER descriptors for polymers or drug molecules using quantum chemically calculated parameters, enabling prediction of hydrophobicity and partition coefficients without experimental input [50].

Workflow Overview:

Step-by-Step Procedure:

• Molecular Structure Definition: Define the molecular structure of interest. For polymers, use the repeating unit as the target structure [50].
• Quantum Chemical Calculation: Perform high-level quantum chemical calculations (e.g., DFT with appropriate functional and basis set) to obtain the electron density distribution and molecular wavefunction [50].
• Electron Density Analysis: Analyze the calculated electron density to extract fundamental molecular properties including atomic partial charges, molecular orbital energies, dipole moment, and polarizability [51].
• Descriptor Calculation: Calculate specific descriptors from the quantum chemical output:
  • Calculate McGowan's characteristic volume (Vx) from computational geometry optimization [12].
  • Derive dipolarity/polarizability (S) from the calculated molecular polarizability and dipole moment [12].
  • Compute hydrogen-bonding acidity (A) and basicity (B) from the surface charge distribution and hydrogen-bonding potential [12].
• Solvation Property Prediction: Use the quantum chemically derived descriptors to predict solvation properties and partition coefficients through established LSER equations [50].
• Abraham Parameter Mapping: Implement the Quantum Chemically Calculated Abraham Parameter (QCCAP) model to map calculated quantum chemical properties to the full set of Abraham parameters [50].
• LSER Model Application: Utilize the predicted Abraham parameters in LSER models to estimate polymer hydrophobicity, drug partitioning, and other physicochemical properties without experimental input [50].

Data Presentation and Analysis

Computational Parameters and Performance Metrics

Table 1: Performance Metrics of Quantum Chemistry-Driven Prediction Models

Prediction Model	System Application	Statistical Performance	Key Advantages	Reference
COSMO-RS Solvation Enthalpy	HB contribution in solute-solvent systems	Good agreement with LSER predictions for most systems	A priori prediction of HB energetics	[14]
QCCAP for Polymer log KOW	Polymer repeating units	RMSE = 0.48 (log scale)	Predicts hydrophobicity from molecular structure alone	[50]
LSER for LDPE/Water Partitioning	156 diverse compounds	R² = 0.991, RMSE = 0.264	High precision for partitioning in polymer systems	[34]
QC-LSER with New Descriptors	Solute-solvent and self-solvation	Improved thermodynamic consistency	Addresses limitations of traditional LSER	[12]

Table 2: Essential Computational Tools for COSMO-RS and LSER Integration

Software Tool	Primary Function	Key Features	Typical Application
COSMOtherm	Property prediction from σ-profiles	Database of pre-calculated solvents; multiple property predictions	Solvation energy, activity coefficients, partition coefficients	[49]
TURBOMOLE	Quantum chemical structure optimization	Efficient DFT calculations; specialized COSMO implementations	Initial geometry optimization; σ-potential calculation	[49]
COSMOconf	Conformer generation and selection	Automated conformation ensemble generation	Boltzmann-weighted conformer sets for accurate property prediction	[49]
QCCAP Model	Abraham parameter prediction	Quantum chemical to LSER descriptor mapping	Predicting parameters for polymers and novel molecules	[50]

Table 3: Key Research Reagent Solutions for COSMO-RS and LSER Implementation

Resource Category	Specific Tool/Parameter	Function/Role in Research	Implementation Note
Computational Software	COSMOtherm Suite	Integrated workflow for COSMO-RS calculations	Commercial license required; multiple versions available	[14] [49]
	TURBOMOLE	Quantum chemical calculations for σ-profiles	Academic licenses available; high performance for DFT	[49]
Reference Databases	LSER Database	Comprehensive solute descriptor repository	Freely accessible; contains thousands of solute parameters	[14] [12]
	HSP Database	Hansen Solubility Parameters for polymers	Useful for comparison and validation studies	[52]
Molecular Descriptors	Hydrogen-Bond Acidity (A)	Quantifies solute H-bond donor strength	Derived from σ-profile hydrogen-bonding regions	[12]
	Hydrogen-Bond Basicity (B)	Quantifies solute H-bond acceptor strength	Obtained from COSMO-RS polarization analysis	[12]
	Dipolarity/Polarizability (S)	Measures solute polarity and polarizability	Calculated from molecular charge distribution	[12]

The integration of quantum chemical calculations, particularly COSMO-RS, with LSER models represents a significant advancement in predictive molecular thermodynamics. This hybrid approach addresses fundamental limitations of traditional LSER by providing a physically grounded, a priori pathway for determining crucial molecular descriptors, especially for hydrogen-bonding interactions [14] [12]. The developed protocols enable researchers to predict key parameters like partition coefficients and solubility with quantifiable accuracy, reducing reliance on extensive experimental screening.

Future developments in this field are likely to focus on several key areas:

• Improved Thermodynamic Consistency: Refinement of LSER equations to ensure proper behavior in self-solvation scenarios and other edge cases [12].
• Expanded Domain Application: Extension of these methods to more complex systems including ionic liquids, deep eutectic solvents, and polymeric materials [48] [50].
• Machine Learning Integration: Combination of quantum chemical descriptors with machine learning algorithms for enhanced prediction accuracy across broader chemical spaces [51].

The ongoing development of COSMO-LSER hybrid models points toward a future where quantum chemical calculations become the standard foundation for predicting solvation parameters, ultimately accelerating drug development, material design, and environmental risk assessment through computationally-driven insight.

The determination of solubility parameters is fundamental to pharmaceutical development, directly influencing drug bioavailability and the design of effective formulations. For decades, the Linear Solvation-Energy Relationships (LSER) model, or the Abraham solvation parameter model, has served as a valuable predictive tool by correlating a solute's free-energy-related properties with its molecular descriptors [9]. This model successfully quantifies solute transfer between phases using linear equations based on descriptors for characteristics like volume, dipolarity, and hydrogen-bonding capacity [9]. However, the extraction of thermodynamically meaningful information from the rich LSER database for use in other molecular thermodynamics developments remains a significant challenge [9].

Machine Learning (ML) presents a transformative opportunity to address this challenge. By leveraging large, high-quality datasets and advanced algorithms, ML models can learn the complex, non-linear relationships between molecular structure and solubility properties that traditional models might approximate linearly. This creates a powerful synergy: the well-established, physically-grounded descriptors from LSER provide a robust feature set for ML models, while ML enhances the predictive accuracy and scope of solubility parameter determination, moving beyond the limitations of linear regression [53] [19]. This integration facilitates a more nuanced understanding of solute-solvent interactions, such as the critical role of hydrogen bonding, which is essential for accurate predictions [54].

Quantitative Comparison of Solubility Prediction Approaches

The evolution from traditional to machine learning methods is marked by a significant increase in predictive performance and application flexibility. The table below summarizes the key characteristics of these different approaches.

Table 1: Comparison of Traditional and Machine Learning-Based Solubility Prediction Methods

Method Type	Examples	Key Inputs/Descriptors	Primary Output	Key Advantages	Reported Performance (Metrics Vary)
Traditional Thermodynamic	Hildebrand Parameter, Hansen Solubility Parameters (HSP) [45]	Cohesive energy density, Dispersion (δd), Polarity (δp), H-bonding (δh) components [45]	Categorical (Soluble/Insoluble) based on "like dissolves like"	Physically intuitive, well-established for polymers	N/A (Categorical prediction)
Linear Free-Energy Relationships	Abraham LSER Model [9]	McGowan’s volume (Vx), excess molar refraction (E), dipolarity/polarizability (S), H-bond acidity (A) and basicity (B) [9]	Partition coefficients (e.g., log P, log K)	Rich in thermodynamic information, provides molecular-level insight	N/A (Model fitting via linear regression)
Equation of State	PC-SAFT [54]	Parameters from binary experimental solubility data [54]	Solubility parameter, Solubility	Explicitly accounts for molecular interactions (e.g., hydrogen bonding) [54]	Provides satisfactory accuracy for drug solubility parameter estimation [54]
Machine Learning (Feature-Based)	XGBoost, Random Forest, CatBoost [53] [19]	Mordred descriptors, features from ESP maps, traditional LSER descriptors [53]	Quantitative Solubility (e.g., logS)	High accuracy, can predict continuous values, handles many features	XGBoost: MAE=0.458, R²=0.918 [53]
Machine Learning (Deep Learning)	Graph Convolutional Networks (GCN), EdgeConv, ANN, CNN [53] [19]	Molecular Graph, 3D Electrostatic Potential (ESP) Maps [53]	Quantitative Solubility (e.g., logS)	Learns directly from molecular structure; no need for pre-defined features	GCN/EdgeConv: Performance generally lower than feature-based XGBoost in comparative studies [53]

The performance of ML models is heavily dependent on the quality and diversity of the training data. For instance, an ensemble model trained on high-quality, curated datasets (ESOL, AQUA, PHYS, OCHEM) not only achieved high accuracy on its test set but also outperformed 37 other models in the Solubility Challenge 2019, demonstrating robust generalization [53]. Furthermore, models like fastsolv, trained on large experimental databases such as BigSolDB, can predict full solubility curves across temperatures and solvents, offering functionality beyond static classification [45].

Protocols for Integrating Machine Learning with LSER-Based Research

Protocol 1: Feature Engineering and Model Training using LSER Descriptors

This protocol details the process of enhancing solubility predictions by using LSER descriptors as inputs for a powerful ML model like XGBoost.

I. Materials and Reagents

• Computational Hardware: A computer workstation with a multi-core CPU (≥8 cores), sufficient RAM (≥16 GB), and a GPU (e.g., NVIDIA RTX series) is recommended to accelerate model training.
• Software Environment: Python (v3.8+) with key libraries: pandas for data handling, rdkit for cheminformatics, mordred for descriptor calculation, xgboost for model training, and shap for model interpretation.
• Data Source: A curated dataset of molecular structures (e.g., in SMILES notation) and their corresponding experimental solubility values (logS). Publicly available datasets include ESOL, AQUA, PHYS, and OCHEM [53].

II. Procedure

• Data Preprocessing:
  • Begin by loading the dataset of SMILES strings and experimental logS values.
  • Standardize the molecular structures using RDKit (e.g., neutralize charges, remove salts) to ensure consistency.
  • Randomly split the entire dataset into a training set (80%) and a held-out test set (20%). The training set will be used for model development and validation, while the test set will provide a final, unbiased evaluation of model performance [53].

• Molecular Representation & Feature Engineering:

  • Calculate LSER-like Descriptors: Use RDKit and the Mordred descriptor package to calculate a comprehensive set of molecular features for each compound. This set will include descriptors that directly correspond to the LSER principles, such as:
    • Vx (Volume): Molecular volume and related topological descriptors.
    • E (Excess Molar Refraction): Calculated refractivity and polarizability descriptors.
    • S (Polarity/Dipolarity): Dipole moment, surface area descriptors, and partial charge metrics.
    • A & B (Hydrogen-Bonding): Hydrogen bond donor and acceptor counts, and related acidic/basic descriptors [53] [9].
  • Feature Selection: Apply a Random Forest-based feature selection method to the calculated descriptors. This technique identifies the most predictive features for solubility, reducing dimensionality and mitigating the risk of overfitting. Retain the top-k most important features for model training [53].

• Model Training and Validation:

  • Initialize Model: Instantiate an XGBoost regressor model.
  • Hyperparameter Tuning: Use a technique like Bayesian optimization or grid search with 5-fold cross-validation on the training set to find the optimal model hyperparameters (e.g., learning rate, max tree depth, number of estimators).
  • Train Final Model: Train the XGBoost model on the entire training set using the optimized hyperparameters.
  • Validate Model: Evaluate the model's performance on the held-out test set by calculating standard metrics: Mean Absolute Error (MAE), Root Mean Squared Error (RMSE), and R-squared (R²). The model should achieve performance metrics similar to or better than those reported in Table 1 (e.g., MAE ≈ 0.46, R² ≈ 0.92) [53].

• Model Interpretation:

  • Apply SHAP (SHapley Additive exPlanations) analysis to the trained XGBoost model.
  • Generate summary plots to identify which LSER-like descriptors (e.g., hydrogen-bonding capacity, molecular volume) are the most significant drivers of the model's predictions, providing transparency and physicochemical insight [53] [19].

The following workflow diagram illustrates this integrated process from data preparation to model interpretation.

Protocol 2: Advanced Representation Learning with 3D Electrostatic Potential (ESP) Maps

This protocol employs deep learning on 3D molecular representations, offering an alternative to pre-defined descriptors by learning features directly from electronic structure.

I. Materials and Reagents

• High-Performance Computing (HPC) Resources: This protocol requires significant computational resources. Access to a cluster with multiple high-core-count CPUs and high-memory nodes is essential for the DFT calculations.
• Software for Quantum Calculations: Gaussian 16 or an equivalent quantum chemistry software package is required for Density Functional Theory (DFT) calculations [53].
• Deep Learning Framework: Python with deep learning libraries such as PyTorch or TensorFlow, and geometric deep learning libraries like PyTorch Geometric for implementing Graph Convolutional Networks (GCN) or PointNet++ (EdgeConv).

II. Procedure

• Generation of 3D Molecular Structures and ESP Maps:
  • Convert SMILES strings to initial 3D coordinates using RDKit's MolFromSmiles module and save them as XYZ files.
  • Perform geometry optimization using DFT in Gaussian 16 at the B3LYP/6-311++g (d, p) level of theory. It is critical to include solvent effects (e.g., water) using the SMD solvation model and empirical dispersion corrections (Grimme-D3) for physiologically relevant and accurate structures [53].
  • From the optimized geometry, calculate the electrostatic potential (ESP) and map it onto the electron density isosurface (cut-off of 0.002 e− bohr−3). The resulting ESP map is a point cloud representation that captures the 3D molecular shape and charge distribution [53].

• Deep Learning Model Implementation:

  • For ESP Maps (Point Cloud): Implement an EdgeConv model, which is designed to learn from point cloud data. The model will learn to extract features directly from the spatial and electrostatic points of the ESP map.
  • For Molecular Graphs: Implement a Graph Convolutional Network (GCN). Represent the molecule as a graph where atoms are nodes and bonds are edges. The GCN will learn features by passing messages across the molecular structure [53].
  • Train both deep learning models on the training set, using the experimental logS values as the target.

• Performance Benchmarking:

  • Evaluate the performance of the deep learning models (EdgeConv and GCN) on the same test set used in Protocol 1.
  • Compare their performance metrics (MAE, RMSE, R²) against the feature-based XGBoost model. Studies indicate that while these models provide valuable insights, their performance may be surpassed by a well-tuned descriptor-based approach like XGBoost [53].

Table 2: Key Computational Tools for ML-Enhanced Solubility Research

Tool/Resource Name	Type	Primary Function in Research	Relevance to LSER/ML Synergy
RDKit	Cheminformatics Library	Converts SMILES to molecules, calculates 2D/3D descriptors, and handles molecular operations.	Fundamental for generating LSER-like molecular descriptors and preparing data for ML models [53].
Mordred	Descriptor Calculator	Calculates a comprehensive set of ~1,800+ molecular descriptors directly from chemical structures.	Automates and expands the calculation of quantitative features that underpin both LSER and ML models [53].
Gaussian 16	Quantum Chemistry Software	Performs DFT calculations to generate optimized 3D geometries and electrostatic potential (ESP) maps.	Provides high-fidelity, quantum-mechanically derived 3D molecular representations for advanced deep learning models [53].
XGBoost	Machine Learning Library	Implements a highly efficient and effective gradient-boosted decision tree algorithm for regression/classification.	Serves as a powerful "off-the-shelf" ML model that can achieve state-of-the-art results using engineered features (e.g., LSER descriptors) [53] [19].
SHAP	Model Interpretation Library	Explains the output of any ML model by quantifying the contribution of each input feature to a prediction.	Bridges the gap between ML "black boxes" and thermodynamic understanding by identifying key physicochemical drivers, akin to interpreting LSER coefficients [53] [19].
Curated Solubility Datasets (ESOL, AQUA, etc.)	Data Resource	Provide high-quality, experimental solubility data for training and validating predictive models.	The foundation of data-driven model development; using multiple curated datasets enhances model robustness and generalizability [53].

The integration of machine learning with the established LSER framework represents a paradigm shift in solubility parameter determination and prediction. By leveraging the rich, physicochemical descriptors of LSER as inputs for powerful, non-linear ML algorithms like XGBoost, researchers can achieve predictive accuracy that surpasses traditional linear models. Furthermore, the use of deep learning on advanced molecular representations such as 3D ESP maps offers a path toward models that learn directly from fundamental electronic structure. The protocols outlined provide a clear roadmap for implementing this synergistic approach, from feature engineering and model training to critical interpretation of results. By adopting these data-driven strategies, pharmaceutical scientists and researchers can accelerate solvent selection, optimize drug formulations, and de-risk the drug development pipeline with more reliable and insightful solubility predictions.

Recommendations for Conducting and Interpreting LSER Studies

The Linear Solvation Energy Relationship (LSER) model, also known as the Abraham model, is a cornerstone predictive tool in solubility and partition coefficient research. Within pharmaceutical sciences, accurately predicting how a drug compound distributes itself between different phases—such as between a polymer container and an aqueous solution, or in biological partitions—is critical for drug development, formulation stability, and predicting bioavailability. The LSER model excels in this domain by quantifying these complex equilibrium processes using a set of chemically intuitive molecular descriptors [34] [9]. The power of LSER lies in its ability to deconstruct a solute's free energy of transfer into contributions from distinct, complementary solute-solvent interactions. This application note provides a detailed protocol for conducting and interpreting LSER studies, framed within the broader context of solubility parameter determination for drug development.

Theoretical Foundation of the LSER Model

The LSER model is built upon the principle that free-energy-related properties of a solute can be correlated with its fundamental molecular descriptors. The model operates primarily through two key linear equations for quantifying solute transfer between phases.

For partitioning between two condensed phases (e.g., water and an organic solvent), the model uses [9]: log(P) = c_p + e_pE + s_pS + a_pA + b_pB + v_pV_x

For partitioning between a gas phase and a condensed phase (solvent), the relationship is [9] [12]: log(K_S) = c_k + e_kE + s_kS + a_kA + b_kB + l_kL

The solute's behavior in these equations is defined by six core molecular descriptors, which are intrinsic properties of the solute molecule. The system's behavior is captured by the lower-case coefficients, which are specific to the solvent or phase system under investigation.

Table 1: LSER Solute Molecular Descriptors

Descriptor	Symbol	Molecular Interaction Represented
McGowan's Characteristic Volume	Vx	Cavity formation energy; endoergic dispersion interactions
Gas-Hexadecane Partition Coefficient	L	General dispersion interactions
Excess Molar Refraction	E	Polarizability from n- and π-electrons
Dipolarity/Polarizability	S	Dipolarity and polarizability interactions
Hydrogen Bond Acidity	A	Solute's ability to donate a hydrogen bond
Hydrogen Bond Basicity	B	Solute's ability to accept a hydrogen bond

The lower-case letters in the equations (e.g., a, b, s) are the system parameters (or LFER coefficients). They represent the complementary properties of the solvent phase and are determined through multilinear regression of experimental partition coefficient data for a diverse set of solute molecules [9]. For instance, a robust LSER model for predicting partition coefficients between low-density polyethylene (LDPE) and water has been established as [34]: log K<sub>i, LDPE/W</sub> = -0.529 + 1.098E - 1.557S - 2.991A - 4.617B + 3.886V

Experimental Protocol for LSER Model Development

Phase I: Experimental Data Collection for Partition Coefficients

The foundation of a reliable LSER model is high-quality, experimentally determined partition coefficient data for a chemically diverse training set of compounds.

• Objective: To measure the equilibrium partition coefficient (P or K) for a wide array of solute molecules between the two phases of interest.
• Critical Considerations:
  • Chemical Diversity: The training set must encompass a broad range of values for all solute descriptors (E, S, A, B, V). This includes non-polar compounds, dipolar compounds, hydrogen-bond donors, and hydrogen-bond acceptors [34].
  • Data Quality: The experimental partition coefficients must be determined accurately at a standardized temperature (typically 298 K). Methods like the saturation shake-flask (SSF) procedure are considered a gold standard for thermodynamic solubility measurement [55].
• Novel Technique Spotlight: Laser Microinterferometry: This method allows for direct observation of the dissolution process and determination of solubility limits and phase transitions.
  • Setup: A thin, wedge-shaped diffusion cell is created between two glass plates, with the solute and solvent placed in contact.
  • Measurement: A laser beam passed through the cell creates an interference pattern. The bending of these fringes near the phase boundary indicates interdiffusion and allows for the quantification of concentration gradients in the diffusion zone.
  • Analysis: Processing of the interferograms enables the construction of concentration profiles and the direct determination of equilibrium solubility and the detection of phase transitions like crystal solvate formation [55].

Phase II: Determination of Solute Descriptors

For each compound in the training set, the six LSER solute descriptors must be known. These can be obtained through two primary routes.

• Route 1: Experimental Determination Existing experimental solute descriptors can be retrieved from curated databases, such as the freely accessible LSER database [9] [12]. This is the preferred method when available, as it provides the highest accuracy.

• Route 2: Computational Prediction When experimental descriptors are unavailable, they can be predicted in silico.

  • QSPR Tools: Various Quantitative Structure-Property Relationship (QSPR) prediction tools can estimate descriptors from a compound's chemical structure [34].
  • Quantum Chemical Calculations: Emerging approaches use quantum chemical calculations (e.g., COSMO-RS) to derive thermodynamically consistent molecular descriptors. These methods can also provide insights into conformational changes upon solvation [12].

Phase III: Model Calibration and Validation

This phase involves constructing the LSER model and rigorously testing its predictive power.

• Multilinear Regression: Perform a multilinear regression analysis, using the experimental partition coefficient as the dependent variable and the six solute descriptors as independent variables. This calculation yields the system-specific coefficients (c, e, s, a, b, v/l) [34] [9].
• Validation Set: A portion of the experimental data (~30%) should be withheld from the initial regression to serve as an independent validation set [34].
• Model Benchmarking:
  • Calculate the partition coefficients for the validation set using the newly derived LSER equation.
  • Perform linear regression of the predicted values against the experimental values.
  • A robust model is indicated by high R² values (>0.98) and low Root Mean Square Error (RMSE) values. Note that predictions based on computed descriptors may have a slightly higher RMSE [34].

Data Interpretation and Analysis

Interpreting System Parameters

The sign and magnitude of the system coefficients provide deep chemical insight into the nature of the phase.

• V and L Coefficients: A positive v or l coefficient indicates that an increase in solute volume favors partitioning into that phase, often seen for hydrophobic phases like LDPE or alkanes [34].
• A and B Coefficients: Negative a and b coefficients signify that the phase is reluctant to engage in hydrogen bonding. A very negative value, as seen in the LDPE/water model for the b coefficient, shows that the phase is a very poor hydrogen-bond acceptor [34].
• Comparative Analysis: By comparing system parameters for different polymers, one can predict their relative sorption behaviors. For example, LDPE, which has negligible hydrogen-bonding capabilities, will exhibit weaker sorption for polar, hydrogen-bonding solutes compared to polymers like polyacrylate (PA) that can offer polar interactions [34].

Table 2: Benchmarking LSER Model Performance (Example: LDPE/Water Partitioning) [34]

Model Input Data	Number of Compounds (n)	Coefficient of Determination (R²)	Root Mean Square Error (RMSE)
Full Training Set	156	0.991	0.264
Validation Set (Experimental Descriptors)	52	0.985	0.352
Validation Set (Predicted Descriptors)	52	0.984	0.511

Connecting LSER to Thermodynamic Properties

The LSER model is rich with thermodynamic information that can be extracted for broader applications. The solvation free energy (ΔG₁₂) obtained from LSER equations is directly linked to the infinite dilution activity coefficient (γ∞), a key parameter in phase equilibrium calculations [9] [12]: ΔG₁₂ / RT = ln( (φ₁⁰ * P₁⁰ * Vm₂) / (γ∞ * RT) ) This connection allows LSER data to inform equation-of-state models and other thermodynamic frameworks, facilitating the estimation of enthalpy and entropy changes upon solvation, particularly for hydrogen-bonding interactions [9] [12].

Table 3: Key Resources for LSER Studies

Resource Category	Specific Tool / Database / Model	Function and Application
Experimental Solute Descriptors	LSER Database [9] [12]	Freely accessible, curated database of experimentally determined solute descriptors.
Computational Descriptor Prediction	QSPR Prediction Tools [34]	Software to predict LSER solute descriptors for novel compounds based on chemical structure.
Quantum Chemical Calculations	COSMO-RS [12]	A-priori predictive tool for solvation quantities; can aid in deriving consistent molecular descriptors.
Advanced Solubility Prediction	PC-SAFT Equation of State [56]	A thermodynamic model that can be used to predict drug solubility parameters, complementing LSER.
Machine Learning for Solubility	Graph Neural Networks (GNNs) [44]	A modern approach for predicting Hansen Solubility Parameters, representing a related but distinct methodology.

Advanced Applications and Integration with Modern Methods

The LSER framework is not static and is being advanced through integration with computational and data-driven approaches. A significant frontier is the thermodynamically consistent reformulation of the model. Current research uses quantum chemical calculations to derive new molecular descriptors for electrostatic interactions, which helps resolve inconsistencies in the model, particularly for self-solvation of associating compounds [12]. Furthermore, the synergy between LSER and machine learning (ML) is growing. While LSER provides chemically interpretable parameters, ML models like Graph Neural Networks (GNNs) can handle complex, non-linear relationships for predicting related properties like Hansen Solubility Parameters [44]. Leveraging the rich thermodynamic information in the LSER database to inform and validate advanced ML models represents a powerful future direction for high-throughput solubility prediction in pharmaceutical development.

Validating LSER Models: Benchmarks and Comparisons with Alternative Methods

Within the framework of Linear Solvation Energy Relationship (LSER) research for solubility parameter determination, experimental validation is the cornerstone of model development and application. The accuracy of in silico predictions, including those derived from the Abraham solvation parameter model, is fundamentally dependent on robust, empirical data gathered from controlled laboratory experiments [9]. This document details two sophisticated techniques—Laser Microinterferometry and Inverse Gas Chromatography (IGC)—that provide critical, high-fidelity data for characterizing solute-solvent interactions, determining thermodynamic solubility, and validating LSER model outputs. These methods are indispensable for researchers and drug development professionals seeking to bridge the gap between theoretical predictions and practical formulation design, particularly for poorly soluble Active Pharmaceutical Ingredients (APIs) [55] [57].

Laser Microinterferometry for Thermodynamic Solubility Profiling

Principle and Relevance to LSER

Laser microinterferometry is a diffusion-based technique that allows for the direct observation of dissolution processes, determination of solubility limits, and detection of phase transitions in real-time [55] [58]. Its relevance to LSER research lies in its ability to provide highly accurate thermodynamic solubility data—the fundamental property that LSER models aim to predict. By quantifying the equilibrium concentration of a solute in a solvent across a temperature range, this method generates the experimental data against which the predictive accuracy of LSER equations, such as log P = cp + epE + spS + apA + bpB + vpVx, can be benchmarked [34] [9]. Furthermore, it can detect the formation of crystalline solvates or amorphous equilibria, phenomena that can significantly impact the interpretation of solubility parameters [55].

Detailed Experimental Protocol

Application Note: Determination of API Thermodynamic Solubility and Phase Behavior.

Objective: To determine the equilibrium solubility and identify phase transitions of an API (e.g., Darunavir) in various pharmaceutical solvents over a temperature range of 25–130 °C [55].

Materials and Reagents:

• API: Amorphous Darunavir (or compound of interest).
• Solvents: High-purity solvents covering a range of polarities and hydrogen-bonding capabilities (e.g., water, glycerol, methanol, ethanol, polyethylene glycol 400, vaseline oil) [55].
• Equipment: Laser microinterferometry setup consisting of a microscope, a temperature-controlled micro-oven, a laser source, a video camera, and a computer for data acquisition [55].

Procedure:

• Sample Preparation: Place a small amount of the API powder and the solvent side-by-side between two glass plates. The inner surfaces of the plates are coated with a thin, translucent metal layer to enhance reflectivity. The plates are fixed with clamps to create a wedge-shaped gap of 60–120 μm [55].
• Mounting and Temperature Equilibration: Secure the diffusion cell into the electric mini-oven attached to the microscope stage. Begin heating or cooling to the desired starting temperature (e.g., 25°C) and allow the system to equilibrate [55].
• Data Acquisition: Illuminate the cell with a monochromatic laser beam. As the components interdiffuse, the changing concentration gradients in the diffusion zone alter the optical density, causing characteristic bending of the interference fringes. Record these interferogram patterns using the video camera [55].
• Interferogram Analysis: Process the captured interferograms to construct concentration profiles across the diffusion zone. The absence of bending indicates insolubility. Bending near the interface indicates limited solubility and amorphous equilibrium. The disappearance of the phase boundary indicates complete miscibility [55].
• Temperature Ramping and Solubility Calculation: Incrementally increase the temperature and repeat steps 3 and 4. The equilibrium solubility at each temperature is determined from the concentration profile at the point of saturation, identified by the interface's stability [55].
• Data Correlation: Compare the obtained solubility data with calculated Hansen solubility parameters to validate the measurements and establish a correlation with molecular-level interactions [55].

Data Presentation and Analysis

Table 1: Solubility Profile of Darunavir in Select Solvents via Laser Microinterferometry [55]

Solvent	Solubility Classification	Observed Phase Behavior	Key Interferogram Feature
Water / Glycerol	Sparingly Soluble	Amorphous equilibrium with Upper Critical Solution Temperature (UCST)	Bending of interference bands near interface
Methanol / Ethanol / Isopropanol	Highly Soluble	Formation of crystalline solvates	Disappearance of interphase boundary
Olive Oil / Vaseline Oil	Practically Insoluble	No significant dissolution	Straight, perpendicular interference bands

Table 2: Dissolution Kinetics of Darunavir at 25°C [55]

Solvent	Relative Dissolution Rate
Methanol	30x
Ethanol	7.5x
Isopropanol	1x (Baseline)

Chromatographic Techniques for Solubility Parameter Determination

Inverse Gas Chromatography (IGC): Principle and Relevance

Inverse Gas Chromatography (IGC) is a powerful technique for characterizing the surface and bulk properties of solid materials, such as polymers, by using well-defined probe vapor molecules [59] [57]. In the context of LSER research, IGC provides direct experimental access to solubility parameters (δ) and Flory-Huggins interaction parameters (χ). These are critical for understanding and predicting polymer-solute interactions and are directly related to the system-specific coefficients (e.g., a, b, s, v) in LSER equations [57] [9]. IGC effectively deciphers the "solvent" properties of a stationary phase (e.g., a polymer excipient), which aligns perfectly with the LSER paradigm of describing phases through complementary system parameters [34] [57].

Detailed Experimental Protocol

Application Note: Determination of Polymer Solubility Parameters and Surface Energy.

Objective: To determine the solubility parameters and surface energy components of polymeric materials (e.g., Polyvinyl Alcohol) using IGC [57].

Materials and Reagents:

• Stationary Phase: Polymer of interest (e.g., PVA2488, PVA2499 powder, >180 mesh) [57].
• Probe Solvents: A series of non-polar and polar solvents of chromatographic purity (e.g., alkanes, dichloromethane, ethyl acetate, ethanol) to probe different interactions [57].
• Support Material: Inert carrier material (e.g., 6201 pickled red carrier, 60-80 mesh) [57].
• Equipment: Gas chromatograph equipped with a flame ionization detector (FID) and a temperature-controlled oven [57].

Procedure:

• Column Preparation: Dissolve the polymer in a volatile solvent (e.g., acetone) and coat it onto the inert support material at a defined ratio (e.g., 1:10 w/w). Pack the coated support into a stainless-steel chromatographic column (e.g., 1.0 m length, 1/8 inch diameter). Condition the column in the chromatograph with carrier gas (Nâ‚‚) at an elevated temperature (e.g., 180°C) for ~24 hours to remove residual solvents and volatiles [57].
• Retention Time Measurement: Set the GC oven to the desired isothermal temperature (e.g., 110°C). Using a gas-tight syringe, inject a small, precise volume (e.g., 0.4 μL) of a probe vapor. Record its retention time. Repeat this process in triplicate for each probe solvent in the series [57].
• Data Calculation - Solubility Parameters:
  • Calculate the net retention volume (Vâ‚™) for each probe from its retention time.
  • For non-polar probes (n-alkanes), the solubility parameter of the polymer (δ₂) can be determined from the maximum in a plot of the specific retention volume (or a related parameter) against the solubility parameter of the probes (δ₁) [59] [57].
• Data Calculation - Surface Energy:
  • The dispersive (non-specific) surface energy (γₛᵈ) of the polymer is determined from the retention data of the n-alkane series.
  • The specific (acid-base) components of surface energy are calculated from the retention data of polar probes, which interact via donor-acceptor mechanisms [57].
• Model Validation: Validate the experimentally obtained solubility parameters using molecular dynamics simulations in software such as Materials Studio, ensuring the chain length of the simulated polymer is sufficient (e.g., ≥30 repeat units) for accuracy [57].

Data Presentation and Analysis

Table 3: IGC-Derived Solubility Parameters and Surface Energy of PVA [57]

Polymer Type	Alcoholysis Degree	Solubility Parameter, δ (MPa^1/2)	Dispersive Surface Energy, γₛᵈ (mJ/m²)	Acid-Base Character
PVA2488	88%	26.5 - 27.5*	Scattered with temperature	Amphoteric, meta-acid
PVA2499	99%	26.5 - 27.5*	Higher than PVA2488	Amphoteric, stronger acidity

Note: The exact value is temperature-dependent and requires experimental determination. The range is indicative based on the study's trends.

Table 4: Key LSER Model Performance Metrics from Literature [34]

LSER Model Application	Data Set	R²	RMSE	Key LSER Equation
LDPE/Water Partitioning	Training (n=156)	0.991	0.264	log Ki,LDPE/W = -0.529 + 1.098E - 1.557S - 2.991A - 4.617B + 3.886V
LDPE/Water Partitioning	Validation (n=52)	0.985	0.352	(Same equation as above)

The Scientist's Toolkit: Key Research Reagent Solutions

Table 5: Essential Materials and Reagents for Solubility and Interaction Studies

Item Category	Specific Examples	Function in Experimentation
Model APIs / Solutes	Darunavir, Cinnarizine, Gefitinib, Triamterene [55] [24]	Act as poorly soluble model compounds for testing solubility enhancement techniques and validating LSER predictions.
Polymeric Stationary Phases	Polyvinyl Alcohol (PVA2488, PVA2499), Low-Density Polyethylene (LDPE) [34] [57]	Serve as the material whose solubility and interaction parameters are characterized using IGC or other techniques.
Probe Solvents for IGC	n-Alkanes (C6-C10), Dichloromethane, Ethyl Acetate, Ethanol, Diethyl Ether [57]	A molecular probe series with known properties to characterize dispersive and specific (acid-base) interactions of a material.
Macrocyclic Hosts	Cucurbit[7]uril [24]	Used in inclusion complexation studies to investigate solubilizing effects on drugs and relate them to LSER-based models.
Chromatographic Supports	6201 Pickling Red Carrier (60-80 mesh) [57]	An inert, high-surface-area solid support used to pack IGC columns with the polymer stationary phase.

Laser Microinterferometry and Inverse Gas Chromatography are two powerful, complementary techniques for the experimental determination of solubility and interaction parameters that are central to developing and validating LSER models. Laser microinterferometry provides a direct window into thermodynamic solubility and phase behavior under dynamic conditions, while IGC offers a precise method for quantifying the cohesive energy and surface characteristics of materials like polymers. For researchers in drug development, mastering these protocols provides a robust experimental foundation. The data generated not only validates the predictions of existing LSER models but also contributes to the expansion and refinement of these models, enhancing their predictive power for formulating challenging, poorly soluble APIs and designing novel polymeric excipients.

Solubility prediction is a cornerstone of research and development in pharmaceuticals, materials science, and chemical engineering. For decades, scientists have relied on conceptual frameworks and quantitative models to predict whether a solute will dissolve in a solvent, guided by the fundamental principle that "like dissolves like" [60]. Two established methodologies for solubility prediction are Linear Solvation Energy Relationships (LSER) and Hansen Solubility Parameters (HSP). The LSER model, particularly in its poly-parameter form (pp-LFER), uses multiple solute descriptors to quantitatively predict partitioning behavior and solvation energies [61] [12]. The Hansen approach characterizes materials with three parameters, defining a "solubility sphere" in three-dimensional space to predict miscibility [4] [45].

This article provides a critical comparison of these two models, framed within the context of ongoing research into robust LSER models for solubility parameter determination. We will delineate their theoretical foundations, present structured comparative data, and provide detailed application protocols to equip researchers with the knowledge to select and implement the appropriate model for their specific challenges.

Theoretical Foundations and Comparative Analysis

Hansen Solubility Parameters (HSP)

Developed by Charles Hansen, the HSP model partitions the total Hildebrand solubility parameter into three distinct components, each representing a specific type of intermolecular interaction [4] [60]:

• Dispersion forces (δD): Originating from transient dipole-induced dipole interactions (London forces).
• Polar interactions (δP): Arising from permanent dipole-dipole interactions between molecules.
• Hydrogen bonding (δH): Representing the energy from hydrogen donor-acceptor interactions.

The core of the HSP methodology lies in calculating the distance (Ra) between two materials (e.g., a polymer and a solvent) in this three-dimensional Hansen space. The formula for this distance is: (Ra)² = 4(δD2 - δD1)² + (δP2 - δP1)² + (δH2 - δH1)² [4].

This Ra is then compared to the interaction radius (R0) of the solute, yielding a Relative Energy Difference (RED):

• RED < 1: High probability of solubility [4]
• RED ≈ 1: Partial solubility or swelling [4]
• RED > 1: Low probability of solubility [4]

HSP's graphical representation via a "Hansen sphere" offers an intuitive visual tool for formulators [45].

Linear Solvation Energy Relationships (LSER)

The LSER model, championed by Abraham, employs a multi-parameter linear equation to describe the transfer of a solute between two phases. For processes such as partitioning from the gas phase to a liquid phase, the model takes the form [12]: Log KG = c + eE + sS + aA + bB + lL

The system coefficients (c, e, s, a, b, l) are solvent- or phase-specific and represent the complementary properties of the phases. They are determined through multilinear regression of extensive experimental data [12]. This approach deconstructs the overall solvation energy into its fundamental molecular interaction contributions, providing profound mechanistic insight.

Critical Comparison of LSER and HSP

The following table summarizes the fundamental characteristics of the LSER and HSP models for direct comparison.

Table 1: Critical Comparison of the LSER and HSP Solubility Models

Feature	Hansen Solubility Parameters (HSP)	Linear Solvation Energy Relationships (LSER)
Theoretical Basis	Empirical, based on cohesive energy density [60]	Semi-empirical, based on linear free-energy relationships [12]
Core Parameters	Three parameters for a material: δD, δP, δH [4]	Six solute descriptors: E, S, A, B, V, L; System coefficients for phases [12]
Primary Output	Relative Energy Difference (RED), categorical (Soluble/Insoluble) [4]	Quantitative partition coefficients (e.g., Log K) and free energies [61] [12]
Molecular Insights	Identifies dominant interaction types (dispersion, polar, H-bonding)	Quantifies contribution of each molecular interaction to the overall process
Handling of Mixtures	Simple weighted average by volume fraction [45]	Requires new regression or estimation for mixture coefficients
Domain of Applicability	Best for polymers, solvents, pigments; struggles with strong H-bonding small molecules [45]	Broadly applicable to any phase partitioning (solvent-polymer, air-water, skin permeation) [61] [12]
Key Limitation	Less quantitative; limited predictive power for complex interactions like solvation [4]	Descriptors often require extensive experimental data for determination [12]

Experimental Protocols

Protocol for Determining Hansen Solubility Parameters of a Novel Polymer

This protocol outlines the empirical method for triangulating the Hansen Solubility Parameters (HSP) and the interaction radius (R0) for an unknown polymer.

Research Reagent Solutions

Table 2: Key Reagents for HSP Determination

Reagent/Solution	Function in Protocol
Solvent Library	A diverse set of 30-40 solvents covering a wide range of δD, δP, δH values. Serves as probes to test solubility behavior.
Test Polymer	The unknown polymer, prepared as small, uniform pieces or powder to ensure consistent surface area and interaction.
Inert Container	Glass vials with seals, providing a inert environment for observing solubility without contamination.

Step-by-Step Workflow

• Sample Preparation: Weigh a small, consistent mass (e.g., 10-50 mg) of the test polymer into a series of clean, labeled glass vials (one vial per solvent).
• Solvent Addition: To each vial, add a precise volume (e.g., 1-2 mL) of a different solvent from the pre-characterized library.
• Equilibration: Seal the vials and agitate gently for a fixed period (typically 24-48 hours) at a constant temperature.
• Visual Assessment: After equilibration, visually inspect each vial and score the result. Common scores are:
  • 1: Complete dissolution (clear solution).
  • 0: Partial dissolution, swelling, or gel formation.
  • -1: No dissolution (polymer remains unchanged).
• Data Analysis: Input the solubility data (scores) and the known HSP values of all solvents into HSP-specific software (e.g., HSPiP). The software will perform an iterative optimization to find the position (δD, δP, δH) and radius (R0) of the "sphere" that best separates the "good" solvents (inside the sphere) from the "poor" ones (outside).

The following workflow diagram summarizes the experimental and computational process for HSP determination:

Protocol for Applying LSER to Predict Sorption to Microplastics

This protocol demonstrates how to use a pre-existing pp-LFER model to predict the distribution coefficient (K) of an organic contaminant between water and aged polyethylene (PE) microplastics, a key process in environmental fate modeling [61].

Research Reagent Solutions

Table 3: Key Reagents and Tools for LSER Prediction

Reagent/Solution	Function in Protocol
Aged PE Microplastics	The sorbent material. UV-aging introduces oxygen-containing functional groups, changing sorption behavior [61].
Organic Contaminant	The solute of interest (e.g., phenol, triclosan).
pp-LFER Equation	The pre-developed model, e.g., Log K = c + vV + lL + ... [61].
Solute Descriptor Database	A database (e.g., UFZ-LSER Database) containing the solute descriptors (V, L, S, A, B) for the contaminant [62].

Step-by-Step Workflow

• Problem Definition: Clearly define the system: "What is the partition coefficient (K) of my solute between water and aged PE?"
• Model Selection: Identify a relevant, validated pp-LFER model from the literature. For this example, we use a model developed for aged PE [61].
• Descriptor Acquisition: Obtain the necessary solute descriptors (V, L, S, A, B) for your organic contaminant from a reputable database such as the UFZ-LSER database [62].
• Calculation: Substitute the solute descriptors and the system coefficients from the selected model into the pp-LFER equation.
• Interpretation: Analyze the calculated Log K value. Furthermore, examine the magnitude of the contributions from each term (vV, lL, etc.) to gain mechanistic insight into the sorption process (e.g., the role of hydrophobic vs. hydrogen-bonding interactions) [61].

The following workflow diagram illustrates the predictive application of an LSER model:

Advanced Applications and Future Directions

LSER in Environmental Chemistry and Microplastics Research

The pp-LFER approach demonstrates particular power in elucidating complex environmental processes. A key application is modeling the sorption of organic contaminants (OCs) onto microplastics (MPs). Research shows that while hydrophobic interactions primarily govern the sorption of OCs to pristine polyethylene (PE), the aging of MPs (e.g., via UV radiation) introduces oxygen-containing functional groups. This aging process increases the importance of polar interactions and hydrogen bonding in the sorption mechanism [61]. Dedicated pp-LFER models developed for aged PE can accurately predict this changed behavior (R² = 0.96), providing a powerful tool for environmental risk assessment where pristine plastic models fail [61].

Integration with Computational Chemistry and Machine Learning

Both LSER and HSP are evolving by integrating with modern computational methods.

• LSER and Quantum Chemistry: A promising direction is the use of quantum chemical (QC) calculations, such as COSMO-RS, to derive LSER molecular descriptors in silico [12]. This QC-LSER hybrid approach aims to overcome the dependency on experimental data for descriptor determination, enabling predictions for novel compounds and ensuring greater thermodynamic consistency [12].
• HSP and Machine Learning: While HSP remains a valuable tool, newer machine learning (ML) models like fastsolv are emerging. These data-driven models can predict actual solubility values (not just categorical outcomes) across a wide range of temperatures and solvents, capturing non-linear effects that are challenging for traditional models [45]. ML models represent a complementary, and in some cases more predictive, approach for complex solubility challenges.

Hansen Solubility Parameters and Linear Solvation Energy Relationships are both powerful yet distinct tools for solubility and partitioning prediction. HSP provides an intuitive, three-dimensional framework that is exceptionally useful for formulators, especially in polymer and coating science, where visual/spatial representation and solvent blending are key. Its primary strength is its conceptual simplicity and ease of application to mixtures.

In contrast, LSER offers a more rigorous, quantitative, and mechanistically insightful framework. Its ability to deconstruct a thermodynamic process into its fundamental molecular interaction contributions makes it invaluable for fundamental research, environmental fate modeling, and any application where a deep understanding of the driving forces is required.

The choice between them is not a matter of which is universally better, but which is more appropriate for the task at hand. For rapid screening of solvents for a polymer, HSP is highly effective. For predicting a quantitative partition coefficient and understanding the specific interactions—such as how the hydrogen bond basicity of a pollutant affects its sorption to aged microplastics—the pp-LFER approach is superior. The future of solubility prediction lies in the continued development of these models, particularly through integration with computational chemistry and machine learning, which will expand their applicability, accuracy, and fundamental insight.

The accurate prediction of solubility behavior is a cornerstone of pharmaceutical and materials development. For decades, the Linear Solvation Energy Relationship (LSER) model, with its strong thermodynamic foundation, has been the principal tool for understanding and predicting solute-solvent interactions. However, the recent rise of machine learning (ML) approaches offers a new paradigm for solubility prediction, often with superior accuracy but reduced interpretability. This application note delineates the core trade-offs between these methodologies, providing researchers with a structured framework for selecting the appropriate tool based on their project's specific needs for accuracy, interpretability, and data availability. The content is framed within the context of a broader thesis on the LSER model for solubility parameter determination, guiding researchers on how to navigate the modern computational landscape.

Theoretical Foundations and Model Mechanics

The LSER Paradigm: A Physicochemical Approach

The LSER model, also known as the Abraham solvation parameter model, is a powerful predictive tool that correlates free-energy-related properties of a solute with a set of six fundamentally derived molecular descriptors [9]. Its success stems from a robust thermodynamic basis that directly links model parameters to specific molecular interactions.

The model operates primarily through two key equations for quantifying solute transfer between phases. For transfer between two condensed phases (e.g., water to an organic solvent), the relationship is [9]: log(P) = c_p + e_pE + s_pS + a_pA + b_pB + v_pV_x

For gas-to-organic solvent partitioning, the equation becomes [9]: log(K_S) = c_k + e_kE + s_kS + a_kA + b_kB + l_kL

The molecular descriptors in these equations represent: V_x (McGowan's characteristic volume), L (gas-hexadecane partition coefficient), E (excess molar refraction), S (dipolarity/polarizability), A (hydrogen bond acidity), and B (hydrogen bond basicity) [9]. The lower-case coefficients (e.g., s_p, a_p, b_p) are system-specific descriptors that reflect the complementary properties of the solvent phase.

A key strength of the LSER approach lies in its direct connection to solubility parameter concepts. Recent advances have established a "one-to-one correspondence" between Partial Solvation Parameters (PSP) and LSER molecular descriptors, creating a bridge that allows information exchange between LSER experimental scales and quantum mechanical calculations [21]. This interconnection enhances the utility of both frameworks for understanding fundamental solvation thermodynamics.

The Machine Learning Paradigm: A Data-Driven Approach

Machine learning models for solubility prediction abandon the explicit parameterization of specific molecular interactions in favor of learning complex, non-linear relationships directly from data. Unlike LSER's fixed parameter set, ML algorithms can incorporate diverse molecular descriptors including molecular fingerprints, quantitative structure-property relationship (QSPR) descriptors, and even raw spectral data [45] [19] [63].

Advanced ML architectures being applied to solubility challenges include:

• Deep Neural Networks (DNNs): Such as the FastSolv model which predicts log₁₀(Solubility) across temperatures and solvent systems [45]
• Ensemble Methods: Including Random Forests, Gradient Boosting Machines (GBM), and Extreme Gradient Boosting (XGBoost) for robust predictions [19]
• Convolutional Neural Networks (CNNs): Which can process structural or spectral data directly [19] [63]
• Hybrid Approaches: Combining multiple data modalities (e.g., FT-IR, XRPD, DSC) in consensus models for enhanced accuracy [63]

The fundamental distinction from LSER lies in ML's treatment of the prediction problem as a pattern recognition task rather than a thermodynamic modeling exercise. While LSER parameters have direct physicochemical meanings, the features learned by complex ML models often represent abstract representations that are not easily interpretable by human researchers.

Table 1: Fundamental Comparison of LSER and Machine Learning Approaches

Characteristic	LSER Model	Machine Learning Models
Theoretical Basis	Thermodynamic principles, linear free-energy relationships	Statistical pattern recognition, non-linear function approximation
Core Parameters	Six specific molecular descriptors (Vx, E, S, A, B, L)	Diverse feature sets (molecular fingerprints, topological indices, quantum chemical descriptors)
Model Interpretability	High - each parameter has specific physicochemical meaning	Variable - from moderate (tree-based models) to low (deep neural networks)
Data Requirements	Moderate - requires experimental determination of descriptors	High - needs large, diverse training datasets
Mathematical Form	Linear equations	Non-linear, potentially highly complex functions

Comparative Performance Analysis: Accuracy vs. Interpretability

Quantitative Performance Metrics

Direct comparisons between LSER and ML approaches reveal distinct performance characteristics. LSER models typically explain 80-90% of variance in solubility data for well-characterized systems, as demonstrated in a study of C₆₀ solubility that covered "more than 81 and 87 % of the variance in the training and test sets, respectively" [64]. This represents strong performance for a method with high interpretability.

Modern ML models consistently achieve superior predictive accuracy. For instance, in polymer solubility parameter prediction, advanced algorithms including Categorical Boosting (CatBoost), Artificial Neural Networks (ANN), and Convolutional Neural Networks (CNN) have demonstrated "superior accuracy shown by the highest R-squared values and the lowest error rates" [19]. The FastSolv model exemplifies this capability, accurately predicting not just categorical solubility but actual solubility values across temperature ranges with quantified uncertainty [45].

A critical advantage of ML approaches is their ability to predict continuous solubility values rather than just categorical miscibility. As noted in analyses of modern tools, "HSP and many other empirical models merely classify whether a molecule is likely to be soluble in a solvent, [while] fastsolv can predict the actual solubility along with non-linear temperature effects" [45].

Interpretability and Scientific Insight

While ML models may offer superior accuracy, LSER maintains a significant advantage in interpretability and mechanistic insight. The LSER framework allows direct decomposition of solubility contributions into specific interaction types:

• Hydrogen bonding interactions quantified through A (acidity) and B (basicity) parameters [65] [9]
• Polar interactions captured by the S (dipolarity/polarizability) parameter
• Dispersion forces represented through V_x and L descriptors
• Electronic interactions reflected in the E (excess refraction) parameter

This decomposition enables rational solvent selection based on understanding which specific molecular interactions drive solubility behavior. For example, LSER analysis of drug molecules like Clozapine can identify whether hydrogen bonding capacity, polar interactions, or dispersion forces dominate solubility limitations [65].

In contrast, many complex ML models operate as "black boxes" with limited transparency into their decision-making processes. While techniques like SHAP (SHapley Additive exPlanations) analysis can provide post-hoc interpretations (as used in one study to determine that "dielectric constant was the most significant factor influencing the solubility parameter of polymers" [19]), these interpretations lack the direct physicochemical basis of LSER parameters.

Table 2: Practical Trade-offs for Research Applications

Research Need	Recommended Approach	Rationale
Mechanistic Understanding	LSER	Provides explicit decomposition of interaction contributions
Maximum Predictive Accuracy	Machine Learning (especially deep learning)	Captures complex, non-linear relationships missed by linear models
Solvent Screening	Hansen Solubility Parameters (extended LSER)	Enables "similarity matching" based on multiple interaction parameters
Limited Training Data	LSER	More robust with smaller datasets due to stronger theoretical constraints
Novel Chemical Space	LSER or simpler ML models	Better extrapolation capability through physically meaningful parameters
Large, Diverse Datasets	Advanced ML models	Leverages pattern recognition capabilities unavailable to linear models
Regulatory Compliance	LSER	Higher interpretability facilitates justification of decisions

Experimental Protocols

Protocol 1: Implementing LSER for Solubility Prediction

Objective: Predict solute solubility in various solvents using the LSER framework and interpret the contribution of specific molecular interactions.

Materials and Reagents:

• Abraham LSER parameter database [9]
• Solvent coefficient tables (e.g., from UFZ-LSER database)
• Computational software (Python/R with statistical packages)
• Experimental solubility data for validation

Procedure:

• Solute Characterization: Obtain or calculate the six LSER molecular descriptors (V_x, E, S, A, B, L) for your target solute using established methods [21] [9]
• Solvent Selection: Identify appropriate solvent coefficients for your target solvents from published databases
• Model Application: Apply the relevant LSER equation (partition-based or gas-to-solvent) based on your prediction needs
• Calculation: Compute the predicted solubility value using the appropriate equation:
  • For water-solvent partitioning: log(P) = c_p + e_pE + s_pS + a_pA + b_pB + v_pV_x
  • For gas-solvent partitioning: log(K_S) = c_k + e_kE + s_kS + a_kA + b_kB + l_kL [9]
• Interpretation: Analyze the relative contributions of each term (A×a, B×b, etc.) to understand which molecular interactions dominate the solubility behavior
• Validation: Compare predictions with experimental data and calculate performance metrics (R², RMSE)

Troubleshooting Tips:

• If descriptors are unavailable for novel compounds, consider group contribution methods or quantum chemical calculations
• For poor predictions in specific solvent classes, verify the applicability domain of the solvent coefficients
• When hydrogen bonding discrepancies occur, examine the complementary nature of A/B parameters between solute and solvent

Protocol 2: Machine Learning-Based Solubility Prediction

Objective: Implement a machine learning workflow for predicting solubility across multiple solvents and temperatures.

Materials and Reagents:

• Molecular structures in standardized format (SMILES, SDF)
• Molecular descriptor calculation software (RDKit, PaDEL, Mordred)
• ML framework (scikit-learn, TensorFlow, PyTorch)
• Solubility dataset (e.g., BigSolDB containing 54,273 measurements) [45]

Procedure:

• Data Curation: Collect and preprocess solubility data, identifying and removing outliers using methods like the Monte Carlo outlier detection algorithm [19]
• Feature Engineering: Calculate molecular descriptors for both solute and solvent, including:
  • Mordred descriptors (1,600+ 2D/3D molecular descriptors)
  • Fingerprint representations (Morgan, RDKit fingerprints)
  • Quantum chemical properties (where feasible)
• Model Selection: Choose appropriate algorithms based on dataset size and complexity:
  • For smaller datasets: Random Forests, Gradient Boosting (XGBoost, CatBoost)
  • For large datasets: Deep Neural Networks (like FastSolv architecture) [45]
• Model Training: Implement appropriate validation strategies:
  • Temporal splitting if time-dependent data
  • Scaffold splitting for novel chemical space assessment
  • Cross-validation with multiple random splits
• Model Evaluation: Assess performance using multiple metrics:
  • R² (coefficient of determination)
  • RMSE (Root Mean Square Error)
  • MAE (Mean Absolute Error)
• Interpretation: Apply explainable AI techniques:
  • SHAP analysis to identify feature importance [19]
  • Partial dependence plots to visualize feature relationships
• Deployment: Implement trained model for predictions with uncertainty quantification

Troubleshooting Tips:

• If model performance plateaus, consider ensemble methods or neural network architectures
• For overfitting, implement regularization or reduce feature dimensionality
• When handling imbalanced data, apply appropriate sampling techniques or loss functions

Table 3: Key Resources for Solubility Prediction Research

Resource Category	Specific Tools/Solutions	Function/Application
LSER Databases	UFZ-LSER Database, Abraham Parameter Databases	Source of solute descriptors and solvent system coefficients [9]
Molecular Descriptor Calculators	RDKit, PaDEL, Mordred	Generation of molecular features for QSPR/ML models [45]
Traditional Solubility Models	HSPiP Software, COSMO-RS	Implementation of Hansen Solubility Parameters and quantum chemical approaches [21] [45]
Machine Learning Frameworks	scikit-learn, TensorFlow, PyTorch, FastSolv	Building and deploying ML models for solubility prediction [45] [19]
Experimental Validation Tools	HPLC with diode array detection, Gravimetric methods	Experimental solubility determination for model validation [65]
Specialized ML Models	CatBoost, XGBoost, LightGBM	High-performance gradient boosting for structured data [19]
Explainable AI Tools	SHAP, LIME, Partial Dependence Plots	Interpreting ML model predictions and feature importance [19]

Workflow Integration and Decision Framework

The choice between LSER and machine learning approaches depends critically on research objectives, data resources, and application constraints. The following workflow diagram illustrates the decision process for selecting the appropriate methodology:

This decision framework emphasizes that LSER remains preferable when mechanistic understanding is the primary goal or when data are limited. Machine learning approaches become increasingly advantageous as data volume grows and when predictive accuracy is the dominant concern. For many practical applications, a hybrid approach that uses ML for initial screening followed by LSER analysis for interpretation may offer the optimal balance of accuracy and insight.

The trade-off between interpretability and accuracy in solubility prediction represents a fundamental consideration for research planning. LSER models provide unparalleled interpretability through their foundation in solvation thermodynamics and explicit parameterization of molecular interactions. Machine learning approaches offer superior predictive accuracy by capturing complex, non-linear relationships but often at the cost of mechanistic transparency.

The choice between these paradigms should be guided by specific research objectives. For fundamental studies of solute-solvent interactions or investigations in data-sparse environments, LSER remains the tool of choice. For high-throughput screening or optimization tasks where accuracy is paramount and substantial training data are available, machine learning approaches provide distinct advantages. As both methodologies continue to evolve, researchers equipped with an understanding of their respective strengths and limitations will be best positioned to advance solubility science in pharmaceutical and materials development.

In the development of Linear Solvation Energy Relationship (LSER) models for solubility parameter determination, robust statistical validation and uncertainty quantification (UQ) are paramount for establishing predictive credibility. These processes ensure that models not only fit existing data but also provide reliable, interpretable predictions for new chemical entities. Within pharmaceutical research, where poor aqueous solubility affects a significant proportion of new drug candidates, the ability to quantify predictive uncertainty directly impacts decision-making in drug formulation and excipient selection [24]. This protocol outlines comprehensive methodologies for assessing the predictive power of LSER models, integrating advanced UQ techniques to deliver trustworthy solubility predictions.

Core Statistical Validation Metrics

A multi-faceted approach to validation is required to thoroughly assess model performance. The following quantitative metrics provide a comprehensive view of predictive power.

Table 1: Key Statistical Metrics for LSER Model Validation

Metric	Formula	Interpretation	Ideal Value
Coefficient of Determination (R²)	1 - (SS_res / SS_tot)	Proportion of variance in the response variable that is predictable from the independent variables.	Close to 1.0
Adjusted R²	1 - [(1 - R²)(n - 1)/(n - p - 1)]	R² adjusted for the number of predictors in the model; penalizes overfitting.	Close to 1.0
Root Mean Square Error (RMSE)	√(SS_res / n)	Measure of the standard deviation of the prediction errors (residuals).	Close to 0
Mean Absolute Error (MAE)	`(Σ	yi - ŷi	) / n`	Average magnitude of the errors in a set of predictions, without considering their direction.	Close to 0

Advanced Uncertainty Quantification Frameworks

Moving beyond simple goodness-of-fit metrics, UQ provides a probabilistic assessment of prediction reliability. Two powerful frameworks are particularly applicable to LSER modeling.

Polynomial Chaos Expansion (PCE) based Response Surface Methodology

The PCE-based Stochastic Response Surface Method (SRSM) is a highly efficient surrogate modeling technique for UQ. It approximates the complex, stochastic LSER physics using computationally inexpensive lower-order polynomial response surfaces [66].

• Principle: Input uncertain parameters (e.g., solute descriptors, solvent parameters) are expressed as functions of a set of standard random variables. The model output (e.g., predicted solubility) is then projected onto a basis of orthogonal polynomials in these random variables [66].
• Advantages:
  • Computational Efficiency: Significantly faster than traditional Monte Carlo Simulation (MCS), requiring far fewer direct model evaluations (e.g., 120 simulations vs. 2000 for MCS) to achieve similar accuracy [66].
  • Integrated Sensitivity Analysis: Sensitivity indices (e.g., Sobol indices), which quantify the contribution of each input parameter's uncertainty to the total output variance, can be evaluated as a byproduct of the PCE without additional computational cost [66].
• Outputs: The method enables a comprehensive stochastic analysis, including parameter correlation studies, percentile range analysis, and the study of higher-order statistical moments (skewness, kurtosis) of the predicted response distribution [66].

Gaussian Process Regression (GPR)

GPR is a non-parametric, Bayesian approach that inherently provides UQ by treating the model response as a probability distribution.

• Principle: A GPR model defines a prior over functions and updates this prior based on training data to form a posterior distribution. For any new input point, it predicts a mean value and an associated variance [67].
• Advantage in Decision-Making: The built-in UQ allows researchers to understand not just the predicted solubility (ȳ(x)), but also the confidence in that prediction (Var[y(x)]). This is critical for identifying the range of process parameters or molecular descriptors that are most likely to yield a desired solubility profile [67].
• Workflow Integration: GPR can be integrated with optimization algorithms to solve the inverse problem—finding the best sets of input parameters (e.g., for a drug molecule) to achieve a target solubility. The optimization can minimize the expected squared deviation, which balances prediction accuracy and uncertainty [67].

Experimental Protocol for Model Validation and UQ

This protocol details the steps for establishing a validated and uncertainty-aware LSER solubility model.

Table 2: Essential Research Reagent Solutions for LSER Solubility Studies

Reagent / Material	Function / Explanation
Cucurbit[7]uril	A macrocyclic host used to form inclusion complexes, improving drug solubility. Offers high binding constant and stability in various pH conditions [24].
Model Drugs (e.g., Gefitinib, Albendazole)	Poorly water-soluble active pharmaceutical ingredients (APIs) with established experimental solubility data, used for model training and validation [24].
Aqueous Buffer Solutions	To maintain a constant pH environment during solubility experiments, ensuring consistent ionization states of the drug and host molecules.
UV-vis Spectrophotometer	For quantitative determination of drug concentration in solution by measuring absorbance at characteristic wavelengths (e.g., 446 nm for VB2, 358 nm for Triamterene) [24].

Protocol Steps:

• Data Set Curation:

  • Collect a balanced data set of drug molecules with experimentally determined solubility values, S (e.g., in μM or g L⁻¹), and their corresponding molecular descriptors (D, E, L from eqn (2) or other LSER parameters) [24].
  • Divide the data into a training set (e.g., 70-80%) for model building and a hold-out test set (e.g., 20-30%) for final validation.

• Model Training:

  • Using the training set, establish the LSER model, typically of the form log S = c + vD + eE + iL, via stepwise regression or other fitting techniques to obtain the coefficients c, v, e, i [24].
  • Simultaneously, train the chosen UQ framework (PCE-RSM or GPR) using the same training data.

• Statistical Validation:

  • Apply the trained model to the training set to calculate the metrics in Table 1 (R², RMSE, etc.). This assesses model fit.
  • Perform cross-validation (e.g., 5-fold or 10-fold) on the training data to evaluate the model's robustness and check for overfitting.
  • Crucially, apply the model to the unseen test set and calculate the same validation metrics. Performance on the test set is the true indicator of predictive power.

• Uncertainty Quantification and Sensitivity Analysis:

  • Use the trained UQ model to generate prediction intervals for new drug candidates.
  • Calculate sensitivity indices (e.g., from PCE or via variance-based methods with GPR) to identify which molecular descriptors contribute most to prediction uncertainty. This insight can guide future data collection efforts to reduce overall uncertainty [66].

• Model Deployment and Monitoring:

  • Deploy the validated model for predicting the solubility of new drug candidates.
  • Implement a strategy for continuous validation as new experimental data becomes available, updating the model as necessary.

Workflow Visualization

The following diagram illustrates the integrated workflow for model development, validation, and application, incorporating the principles of UQ.

Model Development and Validation Workflow

For the critical inverse problem—finding the best molecular parameters to achieve a target solubility—the following decision-making workflow is employed, leveraging UQ.

Inverse Problem Decision Workflow

Comparative Analysis of Solvation Descriptors Across Different Polarity Scales

The accurate prediction of solute-solvent interactions is a cornerstone of pharmaceutical development, influencing critical processes from crystallization to formulation. Solvation descriptors and polarity scales provide the quantitative language for these interactions. This application note details the practical integration of multiple descriptor frameworks—primarily the Linear Solvation Energy Relationship (LSER) model, Hansen Solubility Parameters (HSP), and the Kamlet-Abboud-Taft (KAT) model—for a comprehensive solvation analysis. Framed within broader LSER model research, this guide provides validated protocols for determining these parameters, enabling researchers to correlate and leverage their complementary strengths for superior solvent selection and solubility prediction in drug development.

Theoretical Framework and Key Descriptors

Solvation models dissect the complex phenomenon of "like dissolves like" into quantifiable contributions from specific intermolecular interactions. The following table summarizes the core descriptors across three dominant frameworks.

Table 1: Comparative Overview of Major Solvation Descriptor Frameworks

Framework	Core Descriptors	Molecular Interactions Represented	Primary Application Context
LSER (Abraham Model) [68] [9]	E: Excess molar refractionS: Dipolarity/PolarizabilityA: Hydrogen-Bond Acidity (HBD)B: Hydrogen-Bond Basicity (HBA)V: McGowan's Characteristic Volume	Cavity formation energy, dispersion forces, polarizability, dipole-dipole, hydrogen bonding (donor & acceptor)	Prediction of partition coefficients (P), gas-solvent partitioning (KS), and other free-energy-related properties in diverse biphasic systems.
Hansen Solubility Parameters (HSP) [45] [69]	δd: Dispersionδp: Polarδh: Hydrogen-Bonding	Dispersion forces, permanent dipole-permanent dipole, hydrogen bonding	Predicting polymer solubility, polymer-solvent compatibility, and swelling in paints, coatings, and plastics.
Kamlet-Abboud-Taft (KAT) [69] [70]	π*: Dipolarity/Polarizabilityα: HBD Acidityβ: HBA BasicityET(30): Normalized Solvatochromic Polarity	Dipole-dipole, polarizability, hydrogen bonding (donor & acceptor)	Solvatochromic analysis, correlating solvent effects on reaction rates and equilibria, and interpreting spectroscopic shifts.

The LSER model is particularly powerful due to its two-linear-equation formalism for predicting solute transfer properties. For partitioning between two condensed phases (e.g., water and an organic solvent), the model is expressed as [9]: log(P) = c_p + e_pE + s_pS + a_pA + b_pB + v_pV_x

For gas-to-solvent partitioning, the equation is [9]: log(K_S) = c_k + e_kE + s_kS + a_kA + b_kB + l_kL

In these equations, the uppercase letters (E, S, A, B, V, L) are the solute's descriptors, while the lowercase coefficients (e.g., s_p, a_p, b_p) are system-specific descriptors reflecting the complementary properties of the solvent phase [9].

Experimental Protocols for Descriptor Determination

Protocol 1: Determination of LSER Descriptors via Gas Chromatography (GC)

This protocol outlines the experimental determination of key LSER descriptors (S, A, L) for a solute using a multi-column GC system, as validated by Poole (2024) [68].

1. Principle: The retention behavior of a solute on stationary phases with different polarities and interaction capabilities is related to its molecular descriptors through the solvation parameter model. A multi-column system is required to deconvolute the various interaction contributions.

2. Materials and Reagents:

• Analyte: High-purity compound of interest.
• GC Columns:
  • SPB-Octyl or HP-5: A poly(siloxane) with methyloctyl or dimethyldiphenylsiloxane monomers.
  • Rtx-OPP or DB-210: A poly(siloxane) with methyltrifluoropropylsiloxane monomers.
  • HP-88 or SGE BPX-90: A poly(siloxane) with bis(cyanopropylsiloxane) monomers.
  • DB-WAXetr or HP-INNOWAX: A poly(ethylene glycol) stationary phase.
• Carrier Gas: High-purity Helium or Nitrogen.
• GC System: Equipped with a flame ionization detector (FID) and a precise temperature-controlled oven.

3. Procedure: 1. Prepare dilute solutions of the analyte in a suitable volatile solvent (e.g., methanol). 2. Separately calibrate each of the four GC columns using a homologous series of n-alkanes to determine the column dead time. 3. For each column, inject the analyte and measure its retention factor (k) at multiple temperatures within the range of 60-140°C. A minimum of 20 retention factor measurements across the columns is recommended. 4. The retention factor is calculated as k = (t_R - t₀) / t₀, where t_R is the analyte's retention time and t₀ is the column dead time. 5. Input the measured retention factors and experimental temperatures into a specialized solver algorithm (e.g., the Solver method in Microsoft Excel) that minimizes the difference between the experimental and calculated log(k) values. The calculation uses the following fundamental relationship [68]: log(k) = c + eE + sS + aA + bB + lL 6. The solver optimizes the descriptors S, A, and L for the analyte. The E descriptor for liquids can be calculated independently from the refractive index [68].

4. Data Analysis and Validation:

• The four-column system has been shown to accurately assign S, A, and L descriptors with relative average absolute errors of approximately 3.5%, 0.6%, and 3.2% (for liquids), respectively [68].
• The B descriptor is poorly characterized by this system and requires a stationary phase with hydrogen-bond acid functionality for reliable determination [68].

Protocol 2: Application of KAT-LSER to Model Solubility in Solvent Screening

This protocol uses the KAT-LSER model to correlate and understand the solubility of a solid solute, such as an Active Pharmaceutical Ingredient (API), in a range of pure solvents, as demonstrated for Carprofen and 2,3,4-Trimethoxybenzoic acid (TMBA) [23] [71].

1. Principle: The logarithm of a solute's solubility in different solvents is linearly correlated with the solvent's KAT parameters (π*, α, β). This quantifies the relative influence of solvent dipolarity, HBD acidity, and HBA basicity on the dissolution process.

2. Materials and Reagents:

• Solute: High-purity crystalline solid (e.g., API).
• Solvents: A selection of at least 10-12 organic solvents spanning a wide range of polarity, hydrogen-bond acidity, and basicity (e.g., n-propanol, formic acid, ethyl acetate, water).
• Instrumentation: Analytical balance, thermostated shaking incubator or water bath, HPLC system with UV detector or other suitable analytical instrument for concentration quantification.

3. Procedure: 1. Solubility Measurement: Use a saturation shake-flask method. An excess of the solute is added to each solvent in sealed vials. The vials are equilibrated in a thermostated shaker at a constant temperature (e.g., 298.15 K) for 24 hours or until equilibrium is reached. The solid is then separated from the saturated solution via filtration or centrifugation. 2. Concentration Analysis: Quantify the concentration of the solute in the saturated solution using a calibrated HPLC-UV method or gravimetric analysis. 3. Data Regression: Perform a multiple linear regression analysis of the experimental solubility data (often as log(solubility)) against the known KAT parameters for each solvent. The general model form is [23] [71]: log(S) = C + pπ* + aα + bβ where S is the solubility, C is a constant, and p, a, b are the fitted coefficients that indicate the sensitivity of the solute's solubility to the solvent's dipolarity, acidity, and basicity, respectively.

4. Data Analysis and Interpretation:

• The signs and magnitudes of the coefficients (p, a, b) reveal the molecular interactions governing dissolution. For example, a positive 'a' coefficient indicates solubility increases with solvent HBD acidity, suggesting the solute acts as a strong HBA.
• As seen in TMBA, a dominant positive 'a' coefficient and a negative 'b' coefficient indicate that the solute's solubility is primarily driven by the solvent's ability to donate hydrogen bonds to the solute, while the solvent's basicity may have a slight inhibitory effect [71].

The following workflow diagram illustrates the integrated experimental approach for solvation descriptor determination and application.

Diagram 1: Integrated Workflow for Solvation Analysis

The Scientist's Toolkit: Research Reagent Solutions

Table 2: Essential Materials for Solvation Descriptor Experiments

Item/Category	Specific Examples	Function & Application Note
GC Stationary Phases	SPB-Octyl (HP-5), Rtx-OPP (DB-210), HP-88 (BPX-90), DB-WAXetr (HP-INNOWAX [68]	A multi-column set is essential for deconvoluting and accurately determining the S, A, and L LSER descriptors for a solute.
Solvatochromic Probes	Reichardt's betaine dye, N,N-Dimethyl-p-nitroaniline, p-Nitroaniline, Coumarin 504 [70]	Spectroscopic probes used to experimentally determine the KAT parameters (π*, α, β) of novel or proprietary solvent systems.
Reference Solvents	n-Hexadecane, water, and a suite of well-characterized polar aprotic and protic solvents.	Used for system calibration in GC (n-alkanes for dead time) and for validating model predictions against known partition coefficients.
Model Solute (for method dev.)	Carprofen, 2,3,4-Trimethoxybenzoic acid (TMBA [23] [71]	Well-studied model compounds, ideal for validating new experimental setups for solubility measurement and KAT-LSER modeling.

Data Integration and Comparative Analysis

The true power of a multi-descriptor approach lies in data integration. The following table synthesizes findings from key studies to illustrate how different descriptors explain solubility behavior.

Table 3: Integrated Case Studies of Solvation Descriptor Application

Studied System	Key Findings	Implications for Solvent Selection
Carprofen (CPF) Solubility [23]	KAT-LSER identified strong HBA basicity of CPF as the dominant factor. HSP analysis found optimal solvents have moderate polarity and low cohesion energy.	The ideal solvent for crystallizing CPF is a strong hydrogen-bond donor (e.g., n-propanol, formic acid) that can interact with CPF's HBA sites.
2,3,4-Trimethoxybenzoic Acid (TMBA) Solubility [71]	KAT-LSER model showed a strong positive coefficient for α and a negative for β, indicating solubility is driven by solvent HBD acidity and inhibited by solvent HBA basicity.	Optimal solvents (2-Ethoxyethanol, 2-Methoxyethanol) are those that are strong hydrogen-bond donors to saturate the solute's carboxylic acid group.
DBS Gelation [69]	A comparative study of multiple parameters (HSP, KAT, Catalan, etc.) found that hydrogen-bonding ability (HSP's δh and KAT's α/β) was a much better predictor of gelation ability than general polarity.	Successful gelation depends on specific solute-solvent hydrogen-bonding interactions, not just overall solubility. The directionality of the δh difference is critical.

The synergistic use of LSER, KAT, and HSP descriptors provides a more complete picture of solvation phenomena than any single model alone. The LSER model offers a comprehensive, system-independent framework for predicting partition coefficients, while the KAT-LSER model excels in correlating and rationalizing solubility behavior in pure solvents. HSPs remain invaluable for polymer-solvent compatibility. The experimental protocols detailed herein provide a clear roadmap for researchers to generate robust solvation data, enabling rational solvent selection that accelerates drug development and optimizes pharmaceutical processes.

Conclusion

LSER models provide a powerful, thermodynamically grounded framework for understanding and predicting solubility, offering a unique advantage through their chemically interpretable molecular descriptors. For pharmaceutical researchers, the ability to deconstruct solvation into specific interactions like hydrogen bonding acidity/basicity and polarity is invaluable for rational formulation design, especially for poorly soluble BCS Class II and IV drugs. Future directions point toward a more integrated approach, combining the mechanistic insight of LSERs with the predictive power of machine learning and the fundamental basis of quantum chemical calculations. This synergy will be crucial for accelerating drug development, enabling more accurate in-silico screening of excipients, and designing advanced drug delivery systems with tailored solubility properties, ultimately improving drug bioavailability and development efficiency.

References

• 1. 希爾德布蘭德溶解度參數 [https://zh.wikipedia.org/wiki/%E5%B8%8C%E5%B0%94%E5%BE%B7%E5%B8%83%E5%85%B0%E5%BE%B7%E6%BA%B6%E8%A7%A3%E5%BA%A6%E5%8F%82%E6%95%B0]
• 2. 希尔德布兰德溶解度参数 [https://www.wikiwand.com/zh/articles/%E5%B8%8C%E5%B0%94%E5%BE%B7%E5%B8%83%E5%85%B0%E5%BE%B7%E6%BA%B6%E8%A7%A3%E5%BA%A6%E5%8F%82%E6%95%B0]
• 3. Never use Hildebrand Solubility Parameters [https://hansen-solubility.com/HSP-science/Hildebrand-parameters.php]
• 4. Hansen solubility parameter [https://en.wikipedia.org/wiki/Hansen_solubility_parameter]
• 5. 相容性的溶剂选择及预判材料溶剂兼容性——HSP的应用 [https://www.chemanaly.com/500.html]
• 6. Study on the Calculation Method of Hansen Solubility ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC11991492/]
• 7. Applications of the Hansen solubility parameter for cellulose [https://bioresources.cnr.ncsu.edu/resources/applications-of-the-hansen-solubility-parameter-for-cellulose/]
• 8. Hansen Solubility Parameters [https://hansen-solubility.com/]
• 9. Linear Solvation–Energy Relationships (LSER) and ... [https://www.mdpi.com/2673-8015/3/1/7]
• 10. The chemical interpretation and practice of linear solvation ... [https://pubmed.ncbi.nlm.nih.gov/16889784/]
• 11. "rule of thumb" for estimation of variable values [https://pubs.usgs.gov/publication/70006546]
• 12. Quantum Chemical (QC) Calculations and Linear Solvation ... [https://www.mdpi.com/2673-8015/4/4/37]
• 13. In silico package models for deriving values of solute ... [https://pubmed.ncbi.nlm.nih.gov/36625152/]
• 14. COSMO-RS and LSER models of solution thermodynamics [https://www.sciencedirect.com/science/article/abs/pii/S0167732223017981]
• 15. Solubility, Thermodynamic Parameters, and Dissolution ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC11007714/]
• 16. Solubility determination, mathematical modeling, and ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC11411740/]
• 17. Determination of the Hansen solubility parameters from ... [https://www.sciencedirect.com/science/article/pii/S0167732222014490]
• 18. Solubility Parameter Model - an overview [https://www.sciencedirect.com/topics/engineering/solubility-parameter-model]
• 19. Data-driven frameworks to robustly predict solubility ... [https://www.nature.com/articles/s41598-025-12758-1]
• 20. Partial Solvation Parameters of Drugs as a New ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC6359455/]
• 21. Partial solvation parameters and LSER molecular descriptors [https://www.sciencedirect.com/science/article/abs/pii/S0021961412001024]
• 22. Experimental determination of LSER parameters for a set ... [https://pubmed.ncbi.nlm.nih.gov/18409633/]
• 23. Solubility measurement, modelling, and thermodynamic ... [https://www.sciencedirect.com/science/article/abs/pii/S0167732225018689]
• 24. A LSER-based model to predict the solubilizing effect of ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC9055158/]
• 25. Multifunctional application of supramolecular cucurbiturils ... [https://www.sciencedirect.com/science/article/pii/S0378517325006386]
• 26. A LSER-based model to predict the solubilizing effect ... [https://pubs.rsc.org/en/content/articlelanding/2020/ra/d0ra03394d]
• 27. Synthesis of a Disulfonated Derivative of Cucurbit[7]uril ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC4412466/]
• 28. Machine learning analysis of drug solubility via green ... [https://www.nature.com/articles/s41598-025-11823-z]
• 29. High-Fidelity Prediction of Drug Solubility in Supercritical ... [https://www.sciencedirect.com/science/article/pii/S0928098725003197]
• 30. Characterization of solute-solvent interactions in liquid ... [https://www.sciencedirect.com/science/article/pii/S0003267023008930]
• 31. In Silico High-Performance Liquid Chromatography ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC11983366/]
• 32. Recent Advances in Liquid Chromatography–Mass ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12204688/]
• 33. Chromatography Data Systems: Perspectives, Principles, ... [https://www.chromatographyonline.com/view/chromatography-data-systems-perspectives-principles-and-trends]
• 34. Linear solvation energy relationships (LSERs) for robust ... [https://www.sciencedirect.com/science/article/pii/S0928098722000239]
• 35. Experimental partition coefficients and model calibration [https://pubmed.ncbi.nlm.nih.gov/35150822/]
• 36. Practical Understanding of Partition Coefficients [https://www.chromatographyonline.com/view/practical-understanding-of-partition-coefficients]
• 37. Linear solvation energy relationships (LSERs) for robust ... [https://pubmed.ncbi.nlm.nih.gov/35122951/]
• 38. "Predictive Model Development for Adsorption of Organic ... [https://open.clemson.edu/all_dissertations/1290/]
• 39. Predictive model development for adsorption of aromatic ... [https://pubmed.ncbi.nlm.nih.gov/22747100/]
• 40. DFT-B3LYP Calculation - an overview [https://www.sciencedirect.com/topics/chemistry/dft-b3lyp-calculation]
• 41. Insights from the DFT-Assisted Laser Spectroscopy [https://www.mdpi.com/1420-3049/27/19/6226]
• 42. FT-IR spectroscopy combined with DFT calculation to ... [https://www.sciencedirect.com/science/article/abs/pii/S1386142514001267]
• 43. Linear Solvation Energy Relationships in the ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC3477586/]
• 44. Enhancing Hansen Solubility Predictions with Molecular ... [https://www.sciencedirect.com/science/article/abs/pii/S0169743924001084]
• 45. The Evolution of Solubility Prediction Methods - Rowan Scientific [https://rowansci.com/blog/solubility-prediction-methods]
• 46. Linear solvation energy relationships (LSERs) for robust ... [https://www.sciencedirect.com/science/article/pii/S0928098722000227]
• 47. Solubility determination, mathematical modeling, and ... [https://bmcchem.biomedcentral.com/articles/10.1186/s13065-024-01291-3]
• 48. An overview of HSP and COSMO-RS for computational ... [https://www.sciencedirect.com/science/article/abs/pii/S0165993625001402]
• 49. 2.2. COSMO-RS simulations [https://bio-protocol.org/exchange/minidetail?id=3284960&type=30]
• 50. Quantum chemically calculated Abraham parameters for ... [https://academic.oup.com/etc/article/44/3/653/7974149]
• 51. Revisiting the Use of Quantum Chemical Calculations in ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC9866719/]
• 52. Using Hansen solubility parameters to correlate ... [https://www.sciencedirect.com/science/article/abs/pii/S0008622304001101]
• 53. A machine learning approach for the prediction of aqueous ... [https://pubs.rsc.org/en/content/articlehtml/2024/dd/d4dd00065j]
• 54. Prediction of small-molecule pharmaceuticals solubility ... [https://pubmed.ncbi.nlm.nih.gov/41125148/]
• 55. Laser Microinterferometry for API Solubility and Phase ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12298865/]
• 56. Prediction of Small-molecule Pharmaceuticals Solubility ... [https://www.sciencedirect.com/science/article/pii/S0928098725003367]
• 57. Quantitative Study on Solubility Parameters and Related ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC8586924/]
• 58. Laser Microinterferometry for API Solubility and Phase ... [https://pubmed.ncbi.nlm.nih.gov/40733084/]
• 59. Measurement of solubility parameters by gas-liquid ... [https://www.sciencedirect.com/science/article/abs/pii/S0021967300901353]
• 60. Solubility Parameters: Theory and Application [https://cool.culturalheritage.org/coolaic/sg/bpg/annual/v03/bp03-04.html]
• 61. Mechanistic inferences from empirical and LSER modeling ... [https://www.sciencedirect.com/science/article/abs/pii/S0045653524025955]
• 62. LSER Database [https://www.ufz.de/lserd/]
• 63. Machine learning using multi-modal data predicts the ... [https://pubmed.ncbi.nlm.nih.gov/36682506/]
• 64. New LSER Model Based on Solvent Empirical Parameters ... [https://link.springer.com/article/10.1007/s10953-013-0062-2]
• 65. Measurement and correlation of solubility, Hansen ... [https://www.sciencedirect.com/science/article/abs/pii/S0167732221006218]
• 66. Uncertainty quantification and statistical modeling of ... [https://www.sciencedirect.com/science/article/abs/pii/S152661252200490X]
• 67. Data-Driven Prediction and Uncertainty Quantification of ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC10707097/]
• 68. Determination of solvation parameter model compound ... [https://pubmed.ncbi.nlm.nih.gov/38320433/]
• 69. Comparing and Correlating Solubility Parameters Governing ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC4255276/]
• 70. New linear solvation energy relationships for empirical solvent scales using the Kamlet–Abboud–Taft parameter sets in nematic liquid crystals - PMC [https://pmc.ncbi.nlm.nih.gov/articles/PMC9081637/]
• 71. Solubility measurement and thermodynamic modeling of 2, ... [https://www.sciencedirect.com/science/article/abs/pii/S0021961425001168]